Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 80
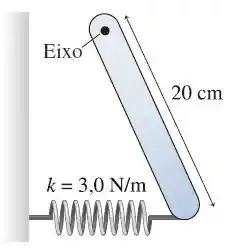
A figura mostra um bastão homogêneo de com um orifício em uma das extremidades. A outra extremidade é presa a uma mola horizontal. Quando o bastão está suspenso exatamente na vertical, a mola não está esticada nem comprimida. Qual será o período de oscilação do bastão? Suponha que a posição angular do bastão em relação à vertical corresponda sempre a um ângulo pequeno.
Passo 1
Se liga! Para resolvermos esta questão precisamos primeiro esquematizar as forças que atuam sobre o bastão. Veja a figura.
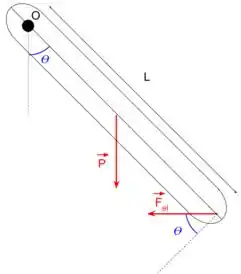
Na figura, o ponto O representa o ponto de rotação. Sabendo que a força peso atua sobre o centro de massa do bastão, podemos escrever a equação do movimento do bastão. Aqui consideraremos que o torque que atua para o bastão girar no sentido horário é negativo. Portanto
Sabendo que
onde
Então
Passo 2
O momento de inércia para um bastão na configuração descrita no problema é
Substituindo (4), (3) e (2) na equação (1), temos
Como a aceleração angular é
Podemos reescrever a equação (5), como
Passo 3
Usando as relações trigonométricas, podemos escrever que
Como estamos trabalhando com pequenas variações de ângulos, podemos escrever que
Sendo assim, podemos substituir estas relações na equação (6), obtendo
Passando tudo para o lado esquerdo, temos
Passo 4
Podemos escrever a equação do oscilado simples como
Repare que a equação (7) é uma típica equação de oscilador harmônico simples. Então podemos fazer a seguinte associação
Passo 5
Como queremos a frequência, temos
Fazendo as devidas conversões e substituindo os valores, temos