Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 86

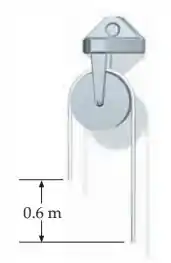
A figura mostra uma polia, na forma de um disco uniforme, por onde passa uma corda. A circunferência da polia é 1.2 m e a sua massa é 2,2 k g . A corda tem 8,0 m de comprimento e sua massa é 4,8 k g . No instante mostrado na figura, o sistema está em repouso e a diferença de altura entre as duas extremidades da corda é 0,60 m . (a) Qual é a rapidez angular da polia quando a diferença de altura entre as duas extremidades da cordas é 7,2 m ? (b) Obtenha uma expressão para a quantidade de movimento angular do sistema, como função do tempo, enquanto nenhuma das extremidades da corda está acima do centro da polia. Não existe deslizamento entre a corda e a polia.

Passo 1

Bora lá, galerinha, essa é pra fechar o capítulo!!! Aí logo agora que tá acabando vem uma bem difícil. Vamos ter que nos preocupar com o peso da corda! Oh não!!! Tô brincando, vem tranquilo que vai ser moleza.

  1. Vamos começar pensando nos tamanhos da corda:

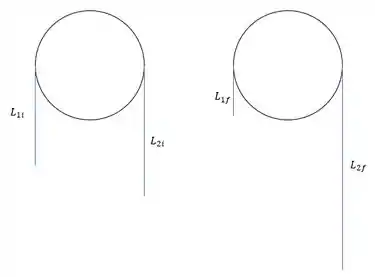
    2. O tamanho total da corda é 7.4 m , então L 1 i + L 2 i = L 1 f + L 2 f = 7.4 m .

    Agora vamos para as diferenças de comprimento que ele deu no enunciado:

    L 2 i - L 1 i = 0.6 m

    L 2 f - L 1 f = 7.2 m

    Juntando essas duas com a primeira, da soma, vamos obter:

    L 1 i = 3.4 m

    L 2 i = 4.0 m

    L 1 f = 0.1 m

    L 2 f = 7.3 m

    Passo 2

    Vamos olhar agora para a conservação de energia. No sistema vamos ter energia potencial gravitacional dos pesos das cordas. Para fazer as contas, vamos considerar o “zero” da energia potencial como a polia, e vamos medir os tamanhos para baixo dela. Vamos considerar que a corda tem densidade linear de massa igual a λ .

    λ = 4.8 k g 8.0 m = 0.6 k g m

    Agora finalmente para a energia:

    Δ U = λ L 1 f g - L 1 f 2 + λ L 2 f g - L 2 f 2 - λ L 1 i g - L 1 i 2 + λ L 2 i g - L 2 i 2

    Arrumando a casa:

    Δ U = - 1 2 λ g ( L 1 f 2 + L 2 f 2 - L 1 i 2 - L 2 i 2 )

    Substituindo valores numéricos:

    Δ U = - 1 2 0.60 9.81 0.1 2 + 7.3 2 - 3.4 2 - 4.0 2

    Δ U = - 75.75 J

    Passo 3

    A energia cinética vai ser:

    K = I p o l i a ω 2 2 + M v 2 2

    Lembrando que v = ω R , e sendo a polia um disco:

    K = M p R 2 ω 2 4 + M ω R 2 2

    K = 1 2 M p 2 + M R 2 ω 2

    Substituindo valores:

    K = 1 2 2.2 2 + 4.8 1.2 2 π 2 ω 2

    K = 0.1076   ω 2

    A variação na energia potencial tornou-se energia cinética. Então essa energia pode ser igualada ao Δ U .

    K = Δ U

    0.1076 ω 2 = 75.75

    ω = 27   r a d / s

    Ufa, que letra (a) mais monstruosa! Falta ainda a (b), então bora lá.

    Passo 4

  2. O momento angular é a soma do momento da polia e da corda.

L = L p + L c

L = I ω + M c R 2 ω

L = 1 2 M p + M c R 2 ω

Se a polia gira de um ângulo Δ θ , a energia potencial vai ser:

U θ = - 1 2 L 1 i - R θ 2 + L 2 i + R θ 2 λ g

Então a variação entre a energia nesse momento e o inicial é:

Δ U = U θ - U 0 = - 1 2 L 1 i - R θ 2 + L 2 i + R θ 2 λ g + 1 2 L 1 i 2 + L 2 i 2 λ g

Δ U = - R 2 θ 2 λ g + L 1 i - L 2 i R θ λ g

No início, em t = 0 , L 1 i ≅ L 2 i , e aí:

Δ U = - R 2 θ 2 λ g

Igualando essa variação à variação de energia cinética:

0.1076 ω 2 - R 2 θ 2 λ g = 0

ω = 1.2 2 π 2 0.6 9.81 0.1076 θ

ω = ( 1.41 s - 1 ) θ

Passo 2

Mas ω é a variação do ângulo no tempo!

ω = d θ d t = 1.41 θ

d θ θ = 1.41 d t

Integrando:

l n θ = 1.41 t

θ t = e 1.41 t

Derivando, para poder achar ω :

ω = d θ d t = 1.41 e 1.41 t

Passo 3

Agora é só colocar isso na expressão do momento de inércia!

L = 1 2 M p + M c R 2 ω

L = 2.2 2 + 4.8 1.2 2 π 2 1.41 e 1.41 t

L = 0.3 e 1.41 t

Resposta

  1. 27 r a d s
  2. L = 0.3 e 1.41 t
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que o ioiô do problema 17 , em vez de rolar a partir do repouso, é arremeçado para baixo com uma velocidade inicial de 1,3 m / s . ( a ) Quanto tempo o ioiô leva para chegar à extremidade da c
No instante t = 0 , o vetor posição de uma partícula de 2 k g em relação à origem é r → = 4 i → - 2 j → . A velocidade da partícula é dada por v → = - 6 t 2 i → para t ≥ 0 em segundos. Qual é ( a ) o
Um disco de polimento, com momento de inércia 1,2.10 - 3 k g m ² ², está preso a uma broca elétrica cujo motor produz um torque de módulo 16 N . m em relação ao eixo central do disco. Com o torque apl
Um disco com um momento de inércia de 7 k g . m ² ² gira como um carrossel sob efeito de um torque variável dado por τ = 5 + 2 t N . m . No instante t = 1 s , o momento angular do disco é 5 k g . m ²
O momento angular de um volante com um momento de inércia de 0,140 k g . m ² ² e relação ao eixo central diminui de 3 para 0,8 k g . m ² / s ² em 1,5 s . ( a ) Qual é o módulo do torque médio em relaç