Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Problemas - Ex. 50
Uma onda transversal sobre uma corda é dada por
- Ache a amplitude, o período, a frequência, o comprimento de onda e a velocidade de propagação dessa onda.
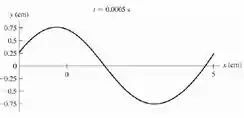
- Faça um desenho da corda para os seguintes valores de : e .
- A onda está se deslocando no sentido ou no sentido ?
- A massa por unidade de comprimento da corda é igual a . Ache a tensão
- Ache a potência média transportada por essa onda.
Passo 1
Letra a)
Olá tudo bem? Vamos começar?
A partir da equação da onda podemos determinar a amplitude, o comprimento de onda e a frequência angular:
A amplitude já identificamos, agora falta determinar comprimento de onda e velocidade de propagação. Vamos começar pelo comprimento de onda. A partir do número de onda:
E a partir da frequência angular, podemos determinar :
O inverso da frequência é o período:
E agora por fim podemos determinar a velocidade de propagação:
Então temos:
Passo 2
Vou deixar os desenhos por últimos. Vamos pular para a letra c)
A onda está se deslocando no sentido negativo de , ou seja, no sentido . Pois a medida que aumenta, para manter o argumento constante, temos que deve ser negativo.
Passo 3
Letra d)
A tensão pode ser dada em função da velocidade de propagação e da densidade linear:
Os valores de velocidade e densidade são respectivamente e , então é só substituir:
Passo 4
Letra e)
A potência média é dada pela seguinte expressão:
E como temos todos esses valores, é só substituir (cuidado com as unidades! Todas devem estar no SI!):
Passo 5
Letra b)
Agora vamos voltar para a letra b). Com a ajuda de um recurso gráfico vamos plotar o gráfico de para primeiro:
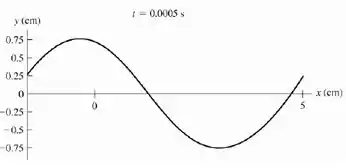
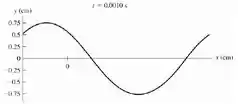
E agora para :
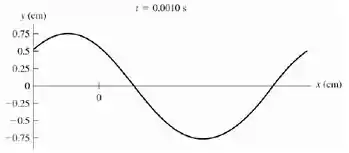
Resposta
