Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 45

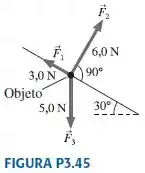
São exercidas três forças sobre um objeto localizado sobre o piso inclinado da FIGURA P3.45. As forças são expressas em newtons (N). Considerando as forças como vetores:

a. Qual é o componente da força resultante F → r e s = F → 1 + F → 2 + F → 3 paralela ao piso?

b. Qual é o componente de F → r e s perpendicular ao piso?

c. Qual é o módulo e qual é a orientação de F → r e s ?

Passo 1

Primeiro passo aqui é visualizar:

Nós conhecemos: F → 1 = 3   N F → 2 = 6   N F → 3 = 5   N θ = 30 ° . E queremos encontrar F → t o t a l , F → t o t a l x e F → t o t a l y .

Use um sistema de coordenadas inclinado para que o e i x o   x desça a inclinação.

Passo 2

Expressando todas as três forças em termos de vetores unitários, temos:

F → 1 = - 3   N i ^ , F → 2 = + 6   N   j ^ e F → 3 = 5   N s e n   θ   i ^ - 5   N cos ⁡ θ   j ^ .

Passo 3

  1. O componente de F → t o t a l paralelo ao chão é:

    2. F t o t a l x = - 3,0   N + 0   N + 5   N sen ⁡ 30 ° = - 0,50 N   o u   0,50   N .

    Passo 4

  2. O componente perpendicular de F   → ao chão é:

    3. F t o t a l y = 0 N + 6 N - ( 5   N cos ⁡ 30 ° ) = 1,67   N .

    Passo 5

  3. A magnitude de F → t o t a l é:

F t o t a l = F t o t a l x + F t o t a l y = - , 050   N 2 + 1,67   N 2 = 1,74   N .

O ângulo F → t o t a l faz é

ϕ = tan - 1 ⁡ F t o t a l y F t o t a l x = tan - 1 ⁡ 1,67   N 0,50   N = 73 °

Está 73 ° acima do piso no lado esquedo de F → 2 .

Resposta

  1. - 0,50 N   o u   0,50   N
  2. 1,67   N
  3. Está 73 ° acima do piso no lado esquedo de F → 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um vento moderado acelera um seixo sobre um plano horizontal x y com uma aceleração constante a = ( 5,00m / s 2 ) i+( 7,00m / s 2 ) j . No instante t = 0 , a velocidade é de ( 4,00m / s ) i . Quais sã
A aceleração de uma partícula é dada por a x ( t ) = - 2,0m / s + ( 3,0m / s 3 ) t . a) Calcule a velocidade inicial v 0 x de modo que a partícula tenha a mesma coordenada x para t = 0 s e t = 4 s . b
Se um objeto está se movendo em uma linha reta com aceleração constante, sua velocidade instantânea no meio de um intervalo de tempo qualquer é (a) maior do que a sua velocidade média, (b) menor do qu
Em uma corrida, em um instante em que dois cavalos estão correndo um ao lado do outro e na mesma direção (a direção + x ), a velocidade e a aceleração instantâneas do cavalo A são + 10m / s e + 2,0m /
A aceleração de uma paraquedista que pula de um avião é dada por a y = g - b v y 2 , onde b é uma constante positiva que depende da área da seção reta da paraquedista e da densidade da atmosfera ao se