Exercícios de Energia Cinética Relativística - Lista de Exercícios Resolvida

A massa de um elétron é . Determine, com seis algarismos significativos, o valor de e o valor de para um elétron com energia cinética .

As massas das partículas envolvidas na reação são as seguintes:

Calcule o da reação.

A energia liberada pela explosão de de é . A massa molar do é . Que peso de seria necessário para liberar uma energia de ?

Esse peso poderia ser carregado em uma mochila ou seria necessário usar um caminhão?

Suponha que na explosão de uma bomba de fissão de massa físsil seja convertida em energia. Que peso de material físsil seria necessário para liberar uma energia de ?

Esse peso poderia ser carregado em uma mochila ou seria necessário usar um caminhão?

Calcule a energia cinética de um próton (massa igual a ) usando a expressão relativística e também a expressão não-relativística e calcule a razão entre os dois resultados (relativística dividida pela não-relativística) para velocidades de

a)

b)

A energia total de um próton é . Calcule a energia cinética () em e a velocidade () desse próton em função de . A energia de repouso do próton é .

Determine a menor energia necessária para transformar um núcleo (cuja massa é ) em três núcleos de (que possuem uma massa de cada um).

A energia total de um próton é . Calcule a energia cinética () em e a velocidade () desse próton em função de . A energia de repouso do próton é .

Uma partícula com massa de repouso , viajando com velocidade ( é a velocidade da luz), colide com uma partícula idêntica inicialmente em repouso.

Após a colisão as duas partículas formam uma única partícula de massa de repouso com velocidade . As respostas devem ser dadas em termos de e de .

1. Calcule a velocidade da partícula resultante.
2. Calcule a massa de repouso dessa nova partícula.
3. Calcule a energia cinética da nova partícula.

Em um acelerador de partículas, uma partícula de massa de repouso é acelerada até ter sua energia cinética igual a 7 vezes a sua energia de repouso. Determine o módulo do momento linear relativístico dessa partícula.

a) .

b) .

c) .

d) .

e) .

Considere as sentenças a seguir sobre a dinâmica relativística aplicada a uma partícula de massa de repouso . Marque a alternativa correta.

a) A força resultante que atua na partícula é igual à derivada do vetor momento linear relativístico dessa partícula em relação ao tempo.

b) A energia cinética relativística de uma partícula é limitada pelo valor .

c) A energia interna dessa partícula vale .

d) O módulo do momento linear relativístico da partícula é limitado pelo valor .

Uma partícula com massa de repouso viaja com velocidade constante de até colidir com uma partícula idêntica, inicialmente em repouso, para um dado referencial inercial. Após a colisão, as duas partículas iniciais formam uma nova partícula.

Em relação ao mesmo referencial inercial, responde o que se pede em função de e de constantes fundamentais.

1. Determine o módulo do momento linear e a energia total da nova partícula
2. Calcule o módulo da velocidade e a massa de repouso da nova partícula.
3. Nesse processo, pode-se dizer que ocorreu conservação da massa de repouso, conversão de energia cinética inicial em massa de repouso ou conversão de massa de repouso do sistema inicial em energia cinética? Justifique sua resposta.

Um átomo absorve um fóton de energia e, após um determinado instante, emite um fóton de energia .

A variação da massa relativística do átomo, considerando as massas após a emissão e antes da absorção, é dada por

As massas das partículas envolvidas na reação são:

; ; ; .

Calcule as massas de repouso do sistema anterior à reação. Faça o mesmo para o sistema produto da reação. Exprima as respostas em u. Admita que as massas de repouso do sistema sejam dadas pela soma das massas dos constituintes, pois para esse cálculo é possível desprezar os termos cinéticos. Calcule o Q da reação.

Um próton se move com velocidade 0,99c. Determine o valor do momento linear p, da energia cinética K e da energia total E,

Um próton se move com velocidade 0,89c. Determine o valor do momento linear p, da energia cinética K e da energia total E desse próton.

Um veículo possui massa de tonelada e quatro rodas de liga leve de massa cada e diâmetro de . Outro veículo idêntico possui rodas de aço de de diâmetro, e mesma massa das de liga leve. Compare a velocidade dos veículos ao final de uma descida de de comprimento e inclinação de . Suponha que ambos veículos tenham velocidade inicial nula.

Uma partícula com energia cinética de e massa de repouso colide inelásticamente com outra partícula de mesma massa em repouso, resultando em uma única partícula após a colisão.

a) Encontre a razão entre a velocidade inicial da partícula incidente e a velocidade da luz.

b) Encontre a razão entre a velocidade da partícula resultante e a velocidade da luz.

c) Encontre a razão entre a massa de repouso da partícula resultante e .

O LHC (Large Hadron Colider) acelera partículas subatômicas a velocidades próximas à da luz para o estudo de colisões relativísticas e produção de matérias através da equivalência massa energia.

Considere duas partículas, inicialmente com massas de repouso iguais a , e se movendo com velocidades de módulos iguais em relação ao laboratório, , e em sentidos opostos, em rota de colisão, como mostra a figura abaixo.

Durante a colisão, as partículas são destruídas e duas novas partículas idênticas, com uma nova massa de repouso são geradas se afastando uma da outra, com velocidade de módulos iguais medidas no laboratório, , como mostra a figura abaixo.

Quando for o caso, deixe a sua resposta em função da velocidade da luz .

1. Sabendo que o diâmetro próprio das partículas originais é de , calcule o valor da sua extensão longitudinal (na direção do movimento) medido no referencial de repouso do LHC.
2. Calcule a massa relativística, em , e o módulo do momento de cada partícula antes da colisão. Calcule a energia relativística total do sistema.
3. Calcule a massa de repouso das novas partículas emergentes, em , após a colisão.
4. A soma das energias cinéticas das partículas antes da colisão é igual à soma das energias cinéticas das partículas depois da colisão? Mostre.

Considere as seguintes afirmações:

1. As transformações de Galileu são obtidas das transformações de Lorentz no limite .
2. A simultaneidade entre dois eventos é relativa ao observador e isso não viola os postulados da relatividade restrita.
3. Em princípio, a energia cinética de uma partícula pode ser tão grande quanto se queira.

1. Nenhuma afirmativa é verdadeira.
2. Apenas é verdadeira.
3. Apenas é verdadeira.
4. Apenas é verdadeira.
5. Apenas e são verdadeiras.
6. Apenas e são verdadeiras.
7. Apenas e são verdadeiras.
8. Todas as afirmativas são verdadeiras.

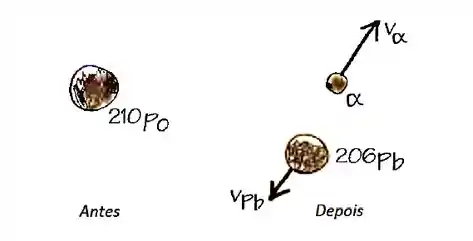
Um isótopo do elemento polônio (símbolo 210Po), com massa igual a , pode decair e dar origem a uma partícula (que é na verdade um núcleo do átomo de hélio) com massa de , e a um isótopo do chumbo (símbolo 206Pb) de massa :

210Po 206Pb

Nesse processo de decaimento, os produtos (206Pb e ) possuem, somados, uma energia cinética de se o átomo de polônio estiver em repouso, que é a situação considerada aqui. Quais as velocidades da partícula e do isótopo 206Pb depois do processo de decaimento? Observe a figura abaixo.

Em uma colisão a altas energias, dois píons e são produzidos no laboratório com velocidades e , respectivamente, na direção , entrando então em um detector de comprimento de .

a) Visto do referencial do píon , qual é o comprimento do detector?

b) Sabendo que píons têm tempo de vida próprio de , conseguirá o píon cruzar todo o detector?

c) Qual é a velocidade do vista do referencial do ?

d) Suponha agora que as velocidades dos píons não são conhecidas e sim os seus momentos, em termos de suas massas de repouso (): e para e , respectivamente. Qual é a razão entre as duas energias cinéticas ?

Uma partícula com massa de repouso e energia total igual duas vezes sua energia de repouso colide com uma partícula , idêntica, em repouso. Após a colisão forma-se uma única partícula com massa de repouso . Nos itens abaixo, expresse suas respostas em termos da velocidade da luz e de .

(a) Calcule a velocidade da partícula antes da colisão.

(b) Calcule a velocidade e a massa da partícula resultante

(c) Calcule a energia cinética da partícula resultante.