Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 11.Problemas - Ex. 8

Pela geometria da elipse, os semieixos maior a e menor b e a semi-distância focal c estão relacionados por a 2 = b 2 + c 2 , e a área da elipse é π a b . (a) Exprima o momento angular L   de um planeta numa órbita elíptica em torno do Sol em função da área A e do período T da órbita, usando a segunda lei de Kepler. (b) Identificando a expressão de L obtida em (a) com a relação entre L , a e a excentricidade da órbita obtida no problema 7, demonstre a terceira lei de Kepler sob a forma T 2 a 3 = 4 π 2 G M s , onde M s é a massa do Sol. (c) O periélio e o afélio de Mercurio são, respectivamente, de 4,59 × 10 7 k m e 6,97 × 10 7 k m , e a massa do Sol é M s = 1,99 × 10 30 k g . Calcule o período da órbita de Mercúrio.

Passo 1

A idéia aqui é dividir a trajetória em pedacinhos triangulares infinitesimais, de base d r e altura r .

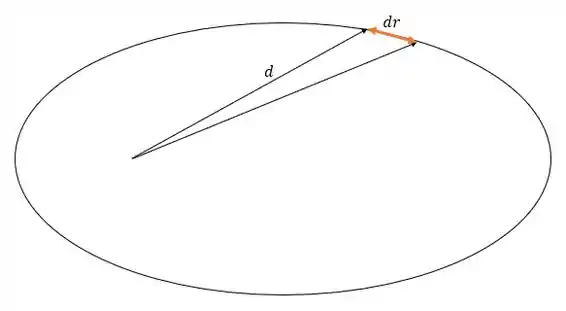
Aí o que a gente vai fazer é integrar a área de todos esses triângulos, pra acharmos a área total!

A = ∫ d ⋅ d r 2

Mas a distância d r é a velocidade vezes o tempo!

A = ∫ d v d t 2

Lembra também que v = d ω , lá do movimento curvilíneo!

A = d ( d ω ) 2 ∫ d t

A = d 2 ω t 2

Só que d 2 ω é justamente o momento angular sobre a massa!!!

A = L t 2

L = 2 A t

Passo 2

O resultado do problema 7 é o seguinte:

e = 1 + L 2 2 m a 2 E

Sabemos da definição das cônicas que:

e = c a

Então:

1 + L 2 2 m a 2 E = c a

1 + L 2 2 m a 2 E = c 2 a 2

L 2 2 m a 2 E = c 2 - a 2 a 2

L 2 2 m E = - b 2

Do resultado do passo 1 :

2 A T 2 = - 2 b 2 m E

4 A 2 T 2 = - 2 b 2 m E

4 π a b 2 T 2 = - 2 b 2 m E

A energia da órbita é calculada por E = - G M m 2 a .

4 π 2 a 2 b 2 T 2 = - 2 b 2 m - G M m 2 a

4 π 2 a 2 T 2 = G M a

Finalmente, com uma arrumada na casa:

T 2 a 3 = 4 π 2 G M

Passo 3

c) Esse a da fórmula é o raio médio, que no caso da elipse, é a média entre o raio do periélio e do afélio!

a = r p + r a 2

a = 5.765 × 10 7 k m

Substituindo na fórmula do item b:

T 2 5.765 × 10 7 × 10 3 3 = 4 π 2 6.67 × 10 - 11 1.99 × 10 30

Resolvendo, obtemos:

T = 88   d i a s

Resposta

  1. L = 2 A t
  2. T 2 a 3 = 4 π 2 G M
  3. T = 88   d i a s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cometa de massa 1,20 × 10 10k g move-se em uma órbita elíptica em torno do Sol. Sua distância do Sol varia entre os intervalos de0,500U A e 50,0U A . (a) Qual é a excentricidade da sua órbita? (b)
O Cometa Halley (Fig. P11.21) aproxima-se do Sol dentro de 0,570U A , e seu período orbital é 75,6a n o s . ( U A é o símbolo da unidade astronômica;1U A=1,50 × 10 11m é a distância média Terra-Sol.)
65 . Estudos sobre a relação do Sol com a nossa galáxia – a Via Láctea – têm revelado que o Sol está localizado próximo da borda externa do disco galáctico, cerca de 30000 anos-luz ( 1a n o - l u z =
64 . O satélite artificial mais antigo em órbita ainda é o Vanguard I, lançado em 3 de março de 1958 . Sua massa é de 1,60k g . Desprezando a resistência do ar, o satélite ainda estaria em sua órbita
62 . Por que a seguinte situação é impossível? Uma nave espacial é lançada em uma órbita circular ao redor da Terra e a circula uma vez por hora.