Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 2.Problemas - Ex. 18
A integral, com limite inferior fixo e limite superior variável, define uma função de ,
Mostre que
Passo 1
Bom, vamos ver um exemplo de integral de uma função para entender qual a ideia do cálculo de uma integral:
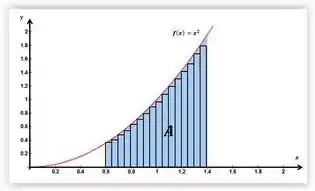
Supondo que queremos calcular a área azul ali.
Ao calcularmos a integral, estaremos somando todas as áreas desses retângulos, ok? Isso porque a integral significa um somatório! Então, se tivermos:
Estaremos calculando a soma de todas as áreas de retângulos embaixo da função, de um ponto até um ponto , ok??
Mas nós podemos escrever essa área do retângulo como , certo? E qual a base de um desses retângulos? É o valor de uma variação em , como estamos vendo retângulos beeeemmmm pequenos, seria um (infinitesimal). E qual o valor da altura? Ora, seria um valor da função num ponto , logo . Então, a área de um retângulo seria:
Ou melhor:
E:
Passo 2
Beleza! Mas a gente sabe, também, que nossa função Área () depende do limite superior da integral, que é varíavel (). Se a gente integra dos dois lados, de um valor fixo até esse variável :
Como a integral de é a soma das áreas, teremos como resultado a própria área :
E olha só!! Ela é igual a , portanto
Como:
O mesmo vale para , portanto:
Obs.: essa é a ideia do Teorema Fundamental do Cálculo! 😊
Prontinho!! Provado!
Resposta
Ei, a resposta está no passo a passo :)