Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 34
Máquinas simples são usadas com frequência para reduzir a força que deve ser exercida para realizar uma tarefa, como a de levantar um grande peso. Tais máquinas incluem o parafuso, sistemas de guincho e alavancas, mas a mais simples das máquinas simples é o plano inclinado. Na figura abaixo, você está erguendo uma caixa pesada para dentro de um caminhão, empurrando-a sobre um plano inclinado (uma rampa). (a) A vantagem mecânica VM do plano inclinado é definida corno a razão da magnitude da força que você teria que aplicar para elevar o bloco na vertical (com rapidez constante) pela magnitude da força necessária para empurrá-lo rampa acima (com rapidez constante). Se o plano não tem atrito, mostre que , onde H é a altura e L é o comprimento da rampa. (b) Mostre que o trabalho que você realiza ao levar a caixa para dentro do caminhão é o mesmo, não importando se vocé o levanta verticalmente ou o empurra rampa (sem atrito) acima.
Passo 1
Letra (a)
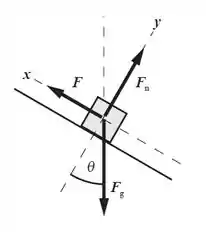
A força que a gente teria que fazer para erguer o bloco na vertical é igual ao peso do bloco (). E a força que teria que fazer para empurrá-lo no plano inclinado é .
Então a vantagem mecânica é dada por:
Passo 2
Olhando para a figura, temos que:
Jogando esse resultado na VM:
Passo 3
Letra (b)
O trabalho que você faz para erguer ao longo do plano inclinado é:
Mas :
Só que perceba que
Passo 4
Calculando o trabalho ergendo o bloco, também teremos:
Só que dessa vez, e :
De fato, os trabalhos deram o mesmo resultado.
Resposta
Ver solução.