Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 28
Uma missão tripulada a Marte, e seus consequentes problemas devido ao tempo extremamente longo que os astronautas passariam sem peso e sem espaço para provisões, tem sido razão de extensa discussão. Para examinar esta questão de maneira simples, consiere uma possível trajetória para a nave: a “órbita de transferência Hohmann”. Esta é uma órbita elíptica tangente à órbita da Terra em seu periélio e tangente à órbita de Marte em seu afélio. Dado que a órbita de Marta tem uma distância média ao Sol igual a vezes a distância média da Terra ao Sol, calcule o tempo gasto pelos astronautas durante a viagem a Marte. Muitos efeitos biológicos adversos (tais como atrofia muscular e decréscimo da massa específica óssea) têm sido observados em astronautas que retornam de órbitas próximas da Terra após apenas alguns meses no espaço. Se fosse o médico de bordo, você deveria estar atento a quais preocupações sobre saúde?
Passo 1
A situação vai ser assim:
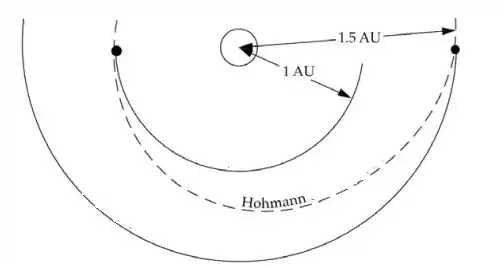
Com a Terra passando da órbita menor para a maior, por meio da órbita de Hohmann.
Pela terceira Lei de Kepler, com o período em anos e o raio em unidades astronômicas:
O tempo de trânsito entre as órbitas é de metade do período:
Além disso, o raio da órbita de Hohmann é o raio médio entre as órbitas.
Então o tempo vai ser:
Que equivale a um período de dias.
Passo 2
O médico de bordo deve programar exercícios com os tripulantes, para que os músculos não atrofiem por falta de uso.
Resposta
dias.