Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 39.Problemas adicionais - Ex. 65

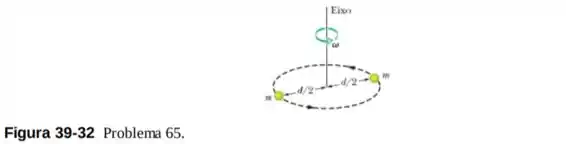
Uma molécula de um gás diatômico é formada por dois átomos de massa separados por uma distância fixa , que giram em torno de um eixo, como mostra a Fig. 39-32. Supondo que o momento angular da molécula é quantizado da mesma forma que no modelo de Bohr do átomo de hidrogênio, determine (a) as velocidades angulares permitidas e (b) as energias rotacionais permitidas.

Passo 1

Fala galerinha, beleza?

O primeiro passo para você resolver esse problema é escrever o momento angular do sistema. Para isso, achamos o momento de inércia com relação ao centro de massa:

O momento angular é dado por

Já a energia cinética rotacional é dada por

Portanto,

Passo 2

Vamos fazer a quantização do momento angular da mesma forma que Bohr fez para o átomo de hidrogênio:

Assim,

Portanto, as possíveis velocidades angulares são

Passo 3

Para achar as energias, basta substituir:

Portanto,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As funções de onda normalizadas para uma partícula confinada a se mover num circulo são: ψ ϕ = 1 2 π 1 2 e - i m ϕ , onde m = 0 , ± 1 , ± 2 , ± 3 , …, e 0 ≤ ϕ ≤ 2 π . Determine ϕ .

Determine quais, entre as seguintes funções, são autofunções do operador inversão i ^ (operador que transforma x → - x ): (a) x 3 - k x ; (b) cos ⁡ k x ; (c) x 2 + 3 x - 1 .Quando for apropriado, dete

Quais, dentre ad funções do Problema 8.15, são (a) também autofunções do operador ( d 2 / d x 2 ) e (b) exclusivamente autofunções de ( d 2 / d x 2 ) ? Dê os autovalores quando for apropriado.

Uma partícula está num estado descrito pela função de onda Ψ = cos ⁡ χ e i k x + sin ⁡ χ e - i k x Onde χ c h i é um parâmetro. Qaul é a probabilidade de a partícula ter o momento linear (a) - k ℏ ; (

Determine quais, entre as seguintes funções, são autofunções do operador d / d x : (a) e i k x ; (b) cos ⁡ k x ; (c) k ; (d) k x (e) e - a x 2 .Nos casos apropriado, determine o correspondente autoval