a) Mostre que para a propagação de uma onda em uma corda a energia cinética por unidade de comprimento da mola é dada por
Onde é a densidade linear.
b) Calcule para uma onda senoidal dada pela Equação (15.7).
c) Existe também energia potencial elástica armazenada na corda associada ao trabalho realizado para esticar e deformar a corda. Considere um pequeno segmento da corda no ponto que possui um comprimento sem deformação igual a , como indicado na Figura 15.13. Desprezando a (pequena) curvatura do segmento, sua inclinação é dada por . Suponha que o deslocamento da corda a partir da posição de equilíbrio seja pequeno, de modo que possui módulo muito menor do que um. Mostre que o comprimento não deformado do segmento é dado aproximadamente por
(Sugestão: use a relação , válida para ).
d) A energia potencial armazenada no segmento é igual ao trabalho realizado pela tensão da corda F ( que atua ao longo da corda) para esticar o segmento desde seu comprimento sem deformação até o comprimento calculado no item (c). Calcule esse trabalho realizado e mostre que a energia potencial por unidade de comprimento da corda é dada por
e) Calcule para uma onda senoidal dada pela Equação (15.7).
f) Mostre que para todos os valores de e de .
g) Faça gráficos de , e em função de para usando os mesmos eixos para as três curvas. Explique por que e assumem alores máximos quando por igual a zero e vice-versa.
h) Mostre que a potência instantânea da onda, dada pela Equação (15.22), é igual a energia total por unidade de comprimento multiplicada pela velocidade da onda . Explique por que esse resultado é razoável.
Passo 1
a) Para mostrarmos que a energia cinética por unidade de comprimento, na propagação de uma onda em uma corda é:
basta fazermos o seguinte calculo:
onde:
e pode ser encntrado a partir da densidade linear da corda:
Portanto a energia cinética será:
Mas podemos escrever em termos da derivada da posição:
Passo 2
b) A Equação 15.7 é:
Para calcular a energia cinética para esta onda vamos primeiro calcular a derivada da posição em função do tempo:
Calculando a energia cinética:
Passo 3
c) Vamos considerar um pedaço da corda com largura e altura . Então para encontrar o comprimento calculamos o módulo da largura e da altura:
Utilizando a aproximação , temos:
Passo 4
d) Para calcular façamos:
Passo 5
e) A Equação 15.7 é:
Para calcular a energia potencial para esta onda vamos primeiro calcular a derivada da posição em função da posição:
Calculando a energia potencial:
Passo 6
f) Temos que ou também podemos escrever .
Mas , então:
Substituindo na energia potencial:
Portanto se olharmos o item (c) veremos que:
Passo 7
g) Gráfico contendo , e :
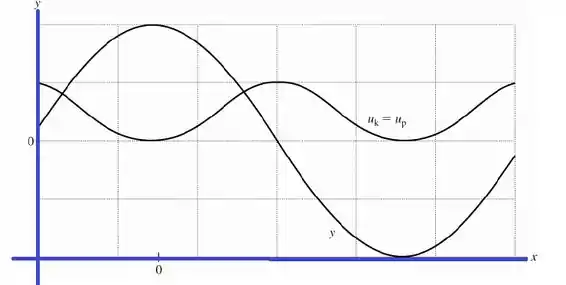
Passo 8
h) Queremos chegar na equação da potência, para isso vamos pegar a energia total por unidade de comprimento multiplicado pela velocidade da onda.
Esse resultado é razoável pois a densidade de energia viaja com a onda, e a taxa na qual a energia é transportada é o produto da densidade por unidade de comprumento e velocidade, que é justamente o que fizemos para encontrar a potencia.
Resposta
Ei, a resposta está no passo a passo :)