Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.2 - Ex. 23
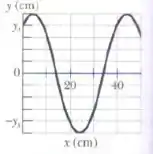
Uma onda transversal senoidal se propaga em uma corda no sentido negativo de um eixo . A figura mostra um gráfico do deslocamento em função da posição no instante ; a escala do eixo é definida por . A tensão da corda é e a massa específica linear é . Determine (a) a amplitude, (b) o comprimento de onda, (c) a velocidade da onda e (d) o período da onda. (e) Determine a velocidade transversal máxima de uma partícula da corda. Se a onda é da forma , determine (f) , (g) , (h) e (i) o sinal que precede
Passo 1
Vamos lá, como o enunciado disse, a função da onda segue essa forma aqui:
No caso, o gráfico representa esse em função de quando , ou seja, a função que está representa no gráfico é:
Vamos ter que analisar o gráfico e essa função pra responder as questões.
Passo 2
(a) A amplitude é simplesmente a altura dos picos da onda (ou dos vales). Em outras palavras, é a distância máxima que a função atinge em relação ao eixo .
No enunciado, nos foi dado que o e se repararmos bem no gráfico, o ocorre no quarto traço do eixo vertical.
Sendo assim, podemos verificar que cada tracinho na nossa escala vertical irá valer um quarto de :
E como a amplitude ocorre no quinto tracinho da escala vertical, nossa amplitude será:
Passo 3
(b) O comprimento de onda é a distância (no eixo ) ocupada por um vale e um pico juntos.
Em outras palavras, é a distância que a onda leva pra se repetir. Olhando o gráfico, dá pra ver que:
Passo 4
(c) A velocidade da onda a gente pode calcular usando os outros valores que a questão também deu:
Usando a fórmula que relaciona esses três valores:
Passo 5
(d) Agora queremos o período da onda. Vamos tentar aproveitar os valores que já temos. Usando a velocidade e o comprimento de onda por exemplo:
Passo 6
(e) Agora queremos a velocidade transversal máxima da onda. A fórmula pra isso é:
Substituindo por
Então agora podemos substituir os valores:
Passo 7
(f) Agora queremos o número de onda , pra isso podemos aproveitar o valor que já calculamos para o comprimento de onda .
Passo 8
(g) A frequência angular nós já até calculamos lá em cima, aproveitando o valor do período :
Passo 9
(h) A fase costuma ser um pouco mais difícil de calcular.
Vamos lembrar qual é a função que está representada no gráfico da questão:
Pegando o ponto em que ela cruza o eixo :
Fazendo isso na calculadora (em radianos) a resposta é:
Passo 10
(i) Pra definir qual é o sinal que acompanha o , é só lembrar daquela relação de sempre:
Então no nosso caso, como a onda se propaga no sentido negativo, o sinal do vai ser positivo.
Resposta
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i) Positivo.