Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 11.Problemas - Ex. 44
Uma nave espacial de massa está em uma órbita circular numa altitude de acima da superfície da Terra. O controle da Missão quer acionar os motores de modo que coloque a nave em uma órbita elíptica em torno da Terra com um apogeu de . Quanto da energia do combustível é necessário ser consumido para alcançar essa órbita? (Suponha que toda a energia do combustível aumentará a órbita. Esse modelo dará um limite inferior para a energia necessária, porque uma parte da do combustível vai se transformar em energia interna dos gases quentes de escape e peças do motor.)
Passo 1
Vem comigo que a gente resolve essa juntos!
A mudança que a nossa nave faz é igual a mostrada na figura do livro, para sabermos quanto de energia do combustível ela gasta para fazer essa mudança, temos que fazer a diferença de energia nave espacial-Terra para a órbita circular e elíptica.
A energia nave espacial-Terra para o caso de uma órbita circular, temos:
Onde vai ser igual ao raio da Terra mais a distância da nave em relação a superfície da Terra, então:
Para uma órbita elíptica, temos:
Onde é o semieixo maior da órbita elíptica.
Só que não conhecemos esse , o podemos calcular de forma rápida somando a distância que o enunciado nos deu com o raio da Terra.
Sobre a órbita elíptica só sabemos o apogeu que é a maior distância entre a Terra e a nave, olhando a seguinte figura podemos tirar uma relação para .
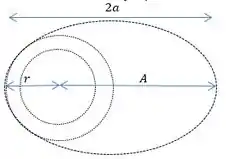
Da imagem tiramos que:
Vamos lá então!
Passo 2
A nossa energia final é a da órbita elíptica e a inicial da circular, assim:
Substituindo com a expressão que temos para , ficamos com:
Assim temos que:
Passo 3
A constante é igual a , e a massa da Terra , agora vamos substituir os valores que temos na expressão que chegamos no passo anterior, lembrando que as distâncias têm que ser em , assim:
Assim temos que:
Então essa foi a energia consumida do combustível para a nave mudar de órbita.