Enunciado
Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 15.Problemas - Ex. 48
Uma onda transversal sobre uma corda é dada por
(a) Ache a amplitude, o período, a frequência, o comprimento de onda e a velocidade de propagação. (b) Faça um desenho da corda para os seguintes valores de e . (c) A onda está se deslocando no sentido ou no sentido ? (d) A densidade linear da corda é igual a . Ache a tensão. (e) Ache a potência média transportada por essa onda.
Passo 1
Faaaaala meu povo, bora iniciar mais um livrinho com a gente!
Para essa questão, primeiramente sabemos que a função de onda de uma onda senoidal que descreve o deslocamento de partículas individuais no meio é dada por:
Onde , e são constantes.
E o sinal de menos é usado quando a onda estar se propagando na direção e o sinal de mais é usado quando a onda está se propagando na direção . A relação entre o número de onda e o comprimento de onda é dada por:
A relação entre a velocidade angular de uma onda e sua frequência é dada por:
A velocidade da onda em uma corda em termos da tensão e da densidade de massa linear é dada por:
E a velocidade da onda em termos de comprimento de onda e frequência é dada por:
Também sabemos que a potência média transportada por uma onda senoidal em uma corda é dada por:
Dados da questão:
A densidade de massa linear da corda é e a função de onda da onda que se propaga na corda é dada por:
Com isso a gente já pode começar nossa questãozinha, então vem comigo!
Passo 2
Letra a)
Se compararmos a função de onda da corda com a função de onda na equação:
, descobriremos que:
O número de onda é:
E a velocidade angular:
Para a frequência, colocamos nosso valor para na relação:
e resolvemos para , então obtemos:
E assim, o período é dado da seguinte forma:
Para o comprimento de onda, colocamos nosso valor para na relação:
, então obtemos:
E finalmente, para a velocidade da onda, colocamos nossos valores para e na equação:
, então obtemos:
Passo 3
Letra b)
As figuras a seguir mostram a forma da corda.
Em :
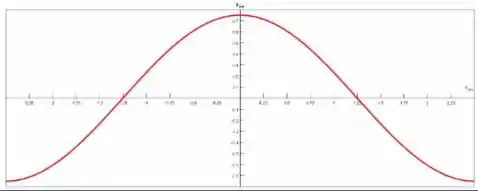
Em :
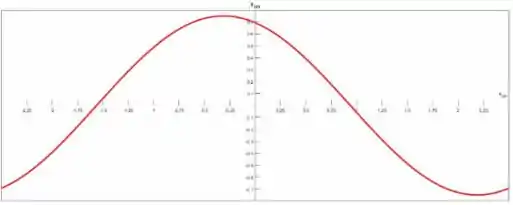
Em :
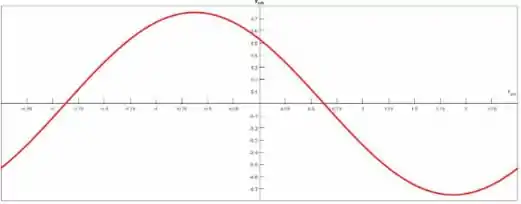
Passo 4
Letra c)
Da equação:
Já que o sinal na função cosseno em frente de na função de onda dada é sinal de mais, então a onda estar se propagando na direção .
Passo 5
Letra d)
Calculamos a tensão na corda substituindo e na equação:
Resolvendo para , então obtemos:
Passo 6
Letra e)
Para cálculo da potência média, basta a gente substituir os dados que já obtemos até aqui, na formula abaixo:
Dessa forma, temos:
E finalmente acabamos nossa questão, deu tudo certinho aí? 😉 Te vejo na próxima!
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
Letra e)