O período de uma partícula oscilando em um movimento harmônico simples é 8.0 s. Em , a partícula está em repouso em . (a) esboce x como função de t, (b) encontre a distância percorrida no primeiro, segundo, terceiro e quarto segundo após
Passo 1
Fala aee, tranquilo??
Beleza, o enunciado pede para esboçarmos a equação do movimento que ele descreve. Uma forma de esboçar um gráfico de em função de é ter a função que relaciona com .
Para um movimento harmônico simples (MHS), que é o movimento que temos no enunciado, a equação que relaciona com tem essa cara:
Onde é a amplitude, que ele já diz ser
E é a frequência angular. Podemos achar ela a partir do período dado no enunciado, pelo seguinte fórmulinha:
Ele diz que :
Vamos substituir e na equação geral do MHS:
Falta só a gente achar , né? Vamos lá!
Passo 2
Cara, falta achar , que é a constante de fase. Mas como?
Nós não usamos duas informações.
- ele diz que em , a partícula está em . Vamos substituir isso na equação que a gente tem até agora:
- Em , a partícula está em repouso, ou seja, . Aqui a gente precisa lembrar que a velocidade é a derivada de , então podemos achar a expressão de e substituir essa última informação
Derivando lembrando da regra da cadeia
Substituindo e :
Um ângulo que satisfaz , ou seja, tem cosseno igual a 1, e satisfaz , ou seja, tem seno igual a zero, é
Passo 3
Nossa equação fica
Esboçando essa belezinha, lembrando que é tempo, então só teremos gráfico em :
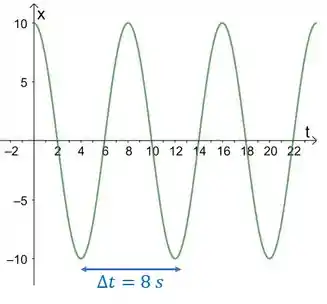
Obs: uma outra forma de construir esse gráfico bonitão é fazer um gráfico com esse formato de ondas, que sai de em , sendo que esse vai ser um pico porque o enunciado deixa claro que essa é amplitude.
E que tenha um período de como ele fala. Como assim? A distância entre dois picos consecutivos das ondinhas desenhadas precisa ser de . Aí chega nesse mesmo resultado, ok?
Passo 4
E na letra b, precisamos calcular a distância percorrida pela partícula dentro do primeiro segundo, ou seja, entre e , depois dentro do segundo segundo, ou seja, entre e , e seguindo esse raciocínio, dentro do terceiro e quarto segundo.
Vamos calcular fazendo
O módulo é porque queremos a distância percorrida e não deslocamento, tudo bem?
Substituindo nossa equação
E substituindo cada valor dado:
Prontinho!! Só isso.
Resposta
(a) 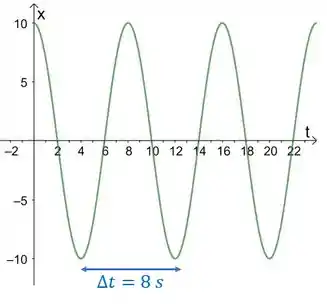
(b) ; ; ; .