Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 65
Uma partícula pontual, de massa , está na origem e uma segunda partícula pontual, de massa , está no eixo em . Determine o campo gravitacional em (a) e (b) . (c) Determine o ponto do eixo para o qual .
Passo 1
Fiz aqui um esquema da configuração dos pontos:
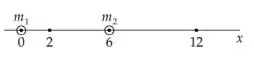
Lembra sempre que a atração gravitacional é no sentido de atração pro corpo que gera ela.
- Sabendo disso, a gente pode deduzir que o campo pra vai ser negativo para a massa e positivo para a massa .
- Agora, por causa da posição, o campo dos dois vai ser negativo em relação ao eixo !
- Esse ponto em que tem que ser no meio dos dois, para que cada massa “puxe para um lado” e possa equilibrar as forças.
Passo 2
Passo 3
Essa equação tem duas soluções, e . Como estamos procurando um ponto entre as massas, a solução vai ser só uma delas!
Resposta
Exercícios de Livros Relacionados
O raio R B de um buraco negro é o raio de uma superfície esférica chamada horizonte de eventos. Nenhuma informação a respeito da região situada no interior do horizonte de eventos pode chegar ao mundo
Um dos primeiros satélites artificiais era apenas um balão esférico de folha de alumínio com 30m de diâmetro e uma massa de 20k g . Suponha que um meteoro com uma massa de 7,0k g passe a 3,0m da super
Quatro esferas homogêneas, de massas m A = 40k g , m b = 35k g , m c = 200k g e m D = 50k g , têm coordenadas ( 0 , 50c m ) , ( 0,0 ) , ( - 80c m ,0 ) e ( 40c m ,0 ) , respectivamente. Em termos dos v
As massas e coordenadas de três esferas são as seguintes: 20k g , x = 0,50m , y = 1,0m ; 40k g , x = - 1,0m , y = - 1,0m ; 60k g , x = 0m , y =- 0,50m . Qual é o módulo da força gravitacional que as t
Você está explorando um planeta recém-descoberto. O raio do planeta é de 7,20X10 7m . Você suspende um peso de chumbo preso à ponta inferior de uma corda leve com 4,00m de extensão e massa de 0,0280k