Um pêndulo físico é formado por uma barra delgada homogênea de comprimento l , suspensa por um ponto à distância s (l / 2 ) de seu centro, oscilando num plano vertical. Para que valor de s o período de oscilação é mínimo? Quanto vale então?

O período de oscilação é mínimo para s = l / 2 3 . Nesse caso o período é τ = 2 π l 3 g .

Enunciado

Vamos começar com um desenho da situação:

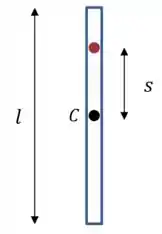
Beleza. Agora vamos imaginar que essa barra oscila em torno do ponto vermelho por um ângulo .

Nesse caso, uma componente da força peso vai puxá-la de volta para a posição original:

E essa força vai agir a uma distância do ponto por está suspensa. Para pequenas oscilações podemos aproximar , então:

Agora precisamos encontrar uma expressão para o momento de inércia em torno do ponto de suspensão.

Vamos usar o teorema dos eixos paralelos, já que conhecemos o momento de inércia quando o eixo passa pelo centro:

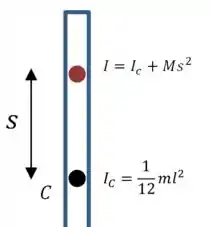
Então:

Agora vamos dividir tudo por e reorganizar um pouco:

Que é a equação de um oscilador harmônico com a seguinte frequência angular:

E o período é:

Ok, agora temos uma expressão para o período em função de . Para achar o ponto de mínimo precisamos derivar e igualar a zero:

Podemos dividir os dois lados pelas constantes:

Como a raiz quadrada é sempre crescente, dá no mesmo procurar o ponto de mínimo do termo que está dentro da raiz:

Agora sim, vamos derivar:

Então esse é o valor que minimiza o período. Nesse caso, o período será:

O período de oscilação é mínimo para . Nesse caso o período é .