Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.Problemas Adicionais - Ex. 97
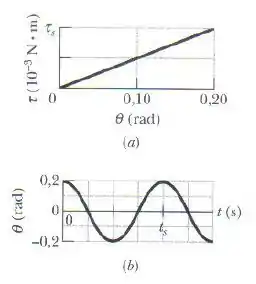
Um pêndulo de torção é formado por um disco de metal com um fio soldado no centro. O fio é montado verticalmente e esticado. A figura mostra o módulo do torque necessário para fazer o disco girar em torno do centro (torcendo o fio) em função do ângulo de rotação . A escala do eixo vertical é definida por . O disco é girado até e depois liberado. A figura mostra a oscilação resultante em termos da posição angular em função do tempo . (a) Qual é o momento de inércia do disco em relação ao centro? (b) Qual é a velocidade angular máxima do disco? [Atenção: não confunda a frequência angular (constante) do MHS e a velocidade angular (variável) do disco, que normalmente são representadas pelo mesmo símbolo, . Sugestão: a energia potencial do pêndulo de torção é igual a , uma expressão análoga à da energia potencial de uma mola, .]
Passo 1
Belezera galerinha, a letra (a) quer que a gente calcule o momento de inércia desse pêndulo. Bora lá ver como fica isso ai.
A fórmula mais simples que a gente conhece pro período do pêndulo de torção é dada como:
Onde é o período, é o momento de inércia e (a letra grega “kappa”) é a constante de torção. Vamos tentar isolar o momento de inércia, que é o que queremos calcular.
Elevando tudo ao quadrado:
Agora isolando:
Beleza.
Passo 2
Pra calcular o momento de inércia precisamos então encontrar o valor de e o período de oscilação. Os gráficos vão nos ajudar, saca só.
O mais tranquilo é o período de oscilação, que é o tempo que o pêndulo demora pra repetir o movimento. Olhando pro segundo gráfico, que tem uma malha quadriculada, dá pra ver que:
E agora pra achar o vamos ter que lembrar da definição dele no pêndulo de torção:
O primeiro gráfico mostra exatamente essa relação ( em função de ), a única diferença é que ele só pega o módulo do torque.
Então para achar o , é só a gente calcular o coeficiente angular da reta no primeiro gráfico, logo:
Portanto:
Passo 3
Agora vamos substituir esse valor, pra gente encontrar o momento de inércia, tal que:
Portanto:
Passo 4
Agora, pra resolver a letra (b) vamos seguir a sugestão do problema. Usar as fórmulas de energia para o pêndulo de torção, bora lá.
Já que a ideia é achar a velocidade angular máxima, vamos usar a lei de conservação de energia e igualar a energia cinética máxima à energia potencial máxima:
Substituindo as fórmulas dessas duas energias no pêndulo de torção:
Temos que tomar cuidado agora, porque esse não é a frequência angular que costumamos representar com ele, na verdade, essa é a velocidade angular, que é a derivada do ângulo em relação ao tempo:
Agora é só isolar o .
No segundo gráfico, dá pra ver que o ângulo máximo que o pêndulo atinge é .
Substituindo isso na fórmula:
Resposta
(a)
(b)