Na pista de um aeroporto fora de operação, um carro de viaja com rapidez constante de . A o arrasto do ar sobre o carro é . Considere que o atrito de rolamento é desprezível. (a) Qual é a força de atrito estático exercida sobre o carro pela superfície da pista, e qual é o mínimo coeficiente de atrito estático necessário para que o carro mantenha essa rapidez? (b) O carro continua a viajar a , mas agora por um caminho com raio de curvatura . Para qual valor de o ângulo entre o vetor da força de atrito estático e o vetor da velocidade será igual a , e para qual valor de ele será igual a ? Qual é o coeficiente de atrito estático mínimo necessário para o carro manter esse último raio de curvatura sem derrapar?

(b) Agora o carro vai percorrer uma trajetória circular, então vamos fazer um esquema para ilustrar a situação:

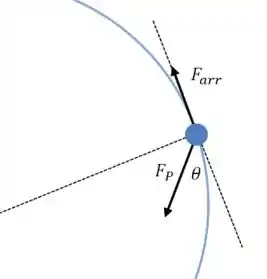
Para manter essa trajetória circular, precisamos de uma resultante centrípeta na direção do centro da trajetória:

E para que o carro viaje com velocidade constante, é preciso que haja equilíbrio na direção da reta tangente ao círculo:

Então ficamos com o seguinte sistema de duas equações:

Queremos calcular no caso em que o ângulo é . Vamos dividir a primeira equação pela segunda:

Onde , e (ou ), então:

E no caso em que :

E qual o coeficiente de atrito estático necessário para que o carro faça essa curva de raio sem derrapar?

Vamos tomar uma das equações do nosso sistema:

E reescrever :

No caso em que , já sabemos que , então:

Como :