Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 24.Exercícios e Problemas - Ex. 18
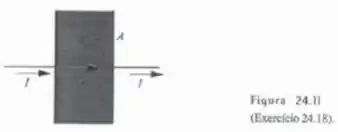
As placas do capacitor de placas paralelas da Figura 24.11 têm área . Sendo e , calcule a densidade de corrente de polarização.
Passo 1
Fala galerinha, beleza?
Você deve ter visto ao longo do capítulo que a corrente de deslocamento pode ser expressa como a derivada temporal do fluxo do campo :
O fluxo do campo dentro do dielétrico é
No capítulo de dielétricos nós vimos que
Assim,
Portanto,
Passo 2
Acontece que a derivada da polarização com relação ao tempo é exatamente a densidade de polarização:
Logo,
Substituindo os valores:
Com isso fechamos o problema 😉.
Resposta
Exercícios de Livros Relacionados
Sendo f r → e V → r → , respectivamente, um campo escalar e um campo vetorial, mostre que ∇ ⋅ f V → = f∇ ⋅ V → + V → ⋅ ∇ f
Mostre que ∇ × ∇ × u → = ∇ ∇ ⋅ u → - ∂ 2 u → ∂ x 2 + ∂ 2 u → ∂ y 2 + ∂ 2 u → ∂ z 2
Considere o campo u → x ,y ,z = zi ^ + xj ^ + yk ^ . Calcule sua divergência e seu rotacional.
Calcule a divergência e o rotacional do campo u → x ,y ,z = x y zi ^ + j ^ + k ^ .
Calcule ∇ × ∇ × V → , onde V → = 1 2 z 2i ^ + x 2j ^ + y 2k ^