Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 14.1 - Ex. 73

Os pontos P 1 e P 2 de um corpo plano distam h 1 e h 2 , respectivamente, do centro de massa. O corpo oscila com o memso período T ao girar livremente em torno de um eixo que passa por P 1 e ao girar livremente em torno de um eixo que passa por P 2 . Estes dois eixos são perpendiculares ao plano do corpo. Mostre que h 1 + h 2 = g T / 4 π 2 , com h 1 ≠ h 2 .

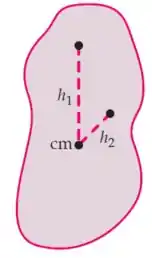
Passo 1

Vamos lembrar da fórmula para o período de um pêndulo físico:

T = 2 π   I m g D

Quando aplicamos essa equação para calcular o período em torno de P 1 , ela vai ficar assim:

T 1 = 2 π I c m + m h 1 2 m g h 1

Onde usamos o teorema dos eixos paralelos para calcular o novo momento de inércia, agora em relação a um eixo que está a uma distância h 1 do centro de massa.

Fazendo a mesma coisa para o período em torno de P 2 :

T 2 = 2 π I c m + m h 2 2 m g h 2

Passo 2

Segundo o enunciado, o período é igual nos dois casos, então:

T 1 = T 2

2 π I c m + m h 1 2 m g h 1 = 2 π I c m + m h 2 2 m g h 2

Vamos dividir os dois lados por 2 π / m g   :

I c m + m h 1 2 h 1 = I c m + m h 2 2 h 2

Agora elevamos os dois lados ao quadrado:

I c m + m h 1 2 h 1 = I c m + m h 2 2 h 2

Vamos simplificar essa expressão para encontrar I c m :

I c m h 1 + m h 1 = I c m h 2 + m h 2

I c m = m h 2 - h 1   1 h 1 - 1 h 2 = m ( h 2 - h 1 ) h 2 - h 1 h 2 h 1

I c m = m h 2 h 1

Passo 3

Precisamos usar esse resultado para encontrar h 1 + h 2 , então vamos voltar à expressão para o período T 1 (como T 1 = T 2 , vamos chamar os dois pelo mesmo nome T ):

T = 2 π I c m + m h 1 2 m g h 1

Elevando tudo ao quadrado e isolando I c m :

m g h 1 T 2 4 π 2 - m h 1 2 = I c m

Agora substituímos a expressão para I c m :

m g h 1 T 2 4 π 2 - m h 1 2 = m h 2 h 1

Dividindo tudo por h 1 :

m g T 2 4 π 2 - m h 1 = m h 2

Agora é só dividir tudo por m e isolar h 1 + h 2 :

h 1 + h 2 = g T 2 4 π 2

Que é exatamente o que queríamos demonstrar.

Resposta

A soma é h 1 + h 2 = g T 2 4 π 2   .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

95. Uma barra uniforme de comprimento L oscila com ângulos pequenos em torno de um ponto situado a uma distância x do seu centro de massa. a ) Prove que a frequência angular é g x / [ L 2 / 12 + x 2 ]
101. Sua medida do período de um pêndulo físico em torno de um dado eixo indica um valor T . A seguir você usa outro eixo de suspensão do lado oposto do centro de massa e encontra o mesmo período. Os
100. Uma régua uniforme de 1,0m está suspensa por uma de suas extremidades em um eixo horizontal e oscila como um pêndulo físico. Um objeto muito pequeno com massa igual à da régua pode permanecer pre
Um bloco retangular, com faces de largura a = 35 c m e comprimento b = 45 c m , é suspenso por uma barra fina que passa por um pequeno furo no interior do bloco e colocado para oscilar como um pêndulo
Dois pêndulos possuem as mesmas dimensões (comprimento L) e massa total (m). O pêndulo A é uma esfera bem pequena oscilando na extremidade de uma barra uniforme de massa desprezível. No pêndulo B, met