O potencial de Morse, que é frequentemente usado para modelar forças interatômicas, pode ser escrito na forma , em que r é a distância entre os dois núcleos atômicos. (a) Usando um programa de planilha ou calculadora gráfica, faça um gráfico do potencial de Morse usando , , e . (b) Determine a separação do equilíbrio e a "constante da mola" para pequenos deslocamentos do equilíbrio para o potencial de Morse. (c) Determine uma expressão para a frequência de oscilação de uma molécula diatômica homonuclear (ou seja, dois dos mesmos átomos), onde cada átomo possui massa m.
Passo 1
Na letra (a) todas as informações sobre o potencial são dadas e precisamos apenas plotar a função do potencial em relação a r:
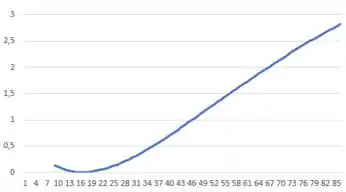
Passo 2
Na letra (b), iremos derivar e igualar a zero o potencial para obtermos a separação do equilíbrio:
Igualando a zero:
Aplicando logaritmo natural dos dois lados:
Que é a separação, com ela iremos calcular a ‘constante da mola’, para isso derivamos novamente:
E aplicando :
Passo 3
Como a equação do potencial para um oscilador harmônico simples é:
Então:
Que é a constante de mola.
Passo 4
Por fim, na (c) vamos utilizar a equação da frequência angular para um sistema massa-mola ( já que a ligação entre duas moléculas pode ser aproximada a isso):
Onde é a massa reduzida do sistema de duas massas, ou seja:
Como a molécula é formada por dois átomos iguais, as massas serão iguais, então:
Substituindo na equação da velocidade angular:
Substituindo k do passo anterior: