Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.6 - Ex. 46
A primeira colisão conhecida entre um fragmento espacial e um satélite artificial em operação ocorreu em 1996: a uma altitude de , um satélite espião francês com um ano de uso foi atingido por um pedaço de um foguete Ariane. Um estabilizador do satélite foi danificado e o satélite passou a girar sem controle. Imediatamente antes da colisão e em quilômetros por hora, qual era a velocidade do pedaço de foguete em relação ao satélite se ambos estavam em órbita circular e (a) a colisão foi frontal e (b) as trajetórias eram mutuamente perpendiculares?
Passo 1
Vamos ver se entendemos a situação. O satélite e o fragmento estão orbitando a terra com o mesmo raio de de órbita.
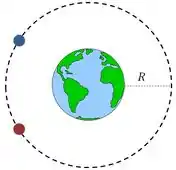
No item (a), queremos saber qual era a velocidade do fragmento em relação ao satélite quando a colisão é frontal. Vamos lembrar da equação que descreve uma órbita circular:
Como podemos consultar a massa da Terra, vamos usar essa fórmula para encontrar a velocidade para o raio de órbita dado (é a mesma para o satélite e o fragmento!).
Passo 2
Preste atenção para não cair na pegadinha clássica de questões de gravitação: o raio da órbita é a distância até o CENTRO DA TERRA. Ou seja, precisamos somar o raio da Terra à altitude dada no enunciado:
Substituindo na fórmula:
Mas o enunciado pede a resposta em quilômetros por hora (é só multiplicar por 3,6!)
Mas ainda não acabou, queremos a velocidade relativa!
Passo 3
Se o satélite e o fragmento, que tem velocidades iguais, sofrerão uma colisão frontal, a velocidade relativa entre eles é simplesmente o dobro de .
Se isso não for intuitivo, lembre-se da fórmula para a velocidade relativa (onde pensamos na velocidade como vetores):
Como as duas velocidades são iguais, e estão na mesma direção e sentidos opostos, uma delas terá sinal negativo e a outra positiva.
Logo:
Passo 4
(b) Agora queremos encontrar esse valor para uma colisão “perpendicular”. Para entender isso, precisamos pensar em três dimensões:
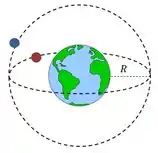
Como o raio das órbitas permanece igual, a única coisa que muda é o cálculo das velocidades relativas. Obviamente, no momento da colisão, os vetores das velocidades serão perpendiculares.
Fazendo a soma vetorial, vemos que o módulo da velocidade relativa será igual ao comprimento da hipotenusa:
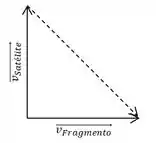
Como calculamos no item anterior , aplicando o teorema de Pitágoras:
Ajustando para três algarismos significativos (seguindo o padrão do enunciado):
Resposta
(a)
(b)