Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.6 - Ex. 59
Três estrelas iguais de massa formam um triângulo equilátero que gira em torno do centro do triângulo enquanto as estrelas se movem ao longo de uma mesma circunferência. O lado do triângulo possui um comprimento L. Qual é a velocidade das estrelas?
Passo 1
A situação é bastante curiosa, então vamos ilustrar a situação:
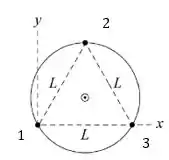
Agora vamos pensar em um par de estrelas desse triângulo. Por exemplo, a força que a estrela faz sobre a estrela (em módulo):
Passo 2
Essa força é um vetor que fica sobre o lado do triângulo que une e . Mas a estrela exerce uma força de mesmo módulo sobre a estrela .
Agora use a regra do paralelogramo pra somar vetorialmente as duas forças.
Você vai ver que o resultado vai ser um vetor que passa pela bissetriz do ângulo, ou seja, pela reta que divide o ângulo ao meio.
E usando um pouco de trigonometria, vemos que o módulo desse vetor vai ser:
Porque os ângulos internos do triângulo equilátero medem , e a bissetriz divide o ângulo ao meio .
Passo 3
Como as estrelas são mantidas em órbita circular pela força gravitacional uma das outras, podemos igualar essa força resultante a uma força centrípeta:
Relacionar e não é muito difícil.
Sabemos que quando um triângulo equilátero de lado está inscrito em uma circunferência de raio :
Substituindo isso na fórmula de cima:
E o resultado é:
Como a questão não deu nenhum valor, a resposta é só essa fórmula mesmo.