Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 39.Problemas - Ex. 58
Para raios X de comprimento de onda igual a 0,0300 nm, o máximo m=1 para um certo cristal ocorre quando o ângulo na figura 36.23c é igual a 35,8°. Em que ângulo o máximo m=1 ocorre quando, em vez dos raios X, usamos um feixe de elétrons de 4,50 keV? Suponha que os elétrons também sofram espalhamento pelos átomos da superfície plana do mesmo cristal.
Passo 1
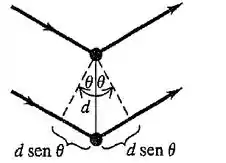
Pela condição de Bragg sabemos que:
Para temos:
Passo 2
Queremos saber qual é o novo ângulo quando usamos feixe de elétrons com .
Podemos então dizer que:
Precisamos descobrir agora quem é .
Passo 3
Se usarmos a relação de De Broglie, podemos relacionar o comprimento de onda com o momento linear.
E como podemos escrever a energia como sendo , o comprimento então será:
Passo 4
Então teremos que:
será:
Como queremos :
Resposta
Exercícios de Livros Relacionados
Calcule ∂ ∂ x , x ^ n para n inteiro.
Use a relação do Problema 1 para calcular x ^ , ∂ 2 ∂ x 2 , a partir de x ^ , ∂ ∂ x .
Demonstre que se A é um operador hermitiano, A 2 ≥ 0 em qualquer estado Ψ .
Para a equação de Schrödinger tridimensional, demonstre o teorema de Ehrenfest : d d tp= -g r a dV
08. Para o movimento num potencial unidimensional V ( x ) , demonstre que, em qualquer estado Ψ , m d d t x ^ 2 Ψ = x ^ p ^ + p ^ x ^ Ψ