Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 16
Um rio tem de largura. Os bancos do rio são retos e paralelos. A corrente está a e é paralela aos bancos. Um barco tem uma rapidez máxima de em águas paradas. O piloto do barco quer andar em linha reta de até , onde a linha é perpendicular aos bancos. O piloto deveria (a) atravessar o rio diretamente em linha reta, (b) seguir contra a corrente da linha , (c) seguir contra a corrente a da linha , (d) desistir, pois a viagem de até não é possível para um barco com esse limite de velocidade, (e) nenhuma dessas alternativas.
Passo 1
Olá, querido! Vamos refletir! A gente tem um barco que quer atravessar em linha reta o rio.
Vamos começar lembrando que quem indica o sentido e direção do movimento é o vetor velocidade resultante. Então para atravessar o rio em linha reta, a gente precisa que o vetor velocidade resultante do barco esteja na direção de AB e no sentido de A para B, ok?
Agora a gente precisa pensar se isso é possível.
A gente entende que esse é o vetor velocidade resultante é em relação ao um referencial no solo, fora do rio, tipo a gente olhando o barco estando fora do rio.
Atuando sobre o barco, temos a correnteza, fazendo com que ele se mova para direita com velocidade . Essa é a velocidade da água em relação ao solo:
E temos a velocidade máxima do barco que está sobre a água, então é uma velocidade do barco em relação a água, que também é de , e a gente vai escolher a orientação.
A velocidade resultante do barco (que é a velocidade so barco em relação ao solo) é a soma vetorial dessas duas velocidades
O que queremos saber é se é possível que exista e esteja na direção e sentido AB.
Passo 2
Para fazer isso, podemos desenhar os vetores das velocidades e
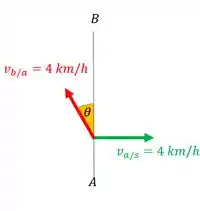
Colocamos numa orientação genérica porque a gente que vai escolher sua orientação.
O essencial aqui é perceber que a rapidez máxima do barco é igual à rapidez da corrente, ou seja, esses dois vetores possuem o mesmo módulo.
Isso quer dizer que o melhor que o piloto do barco pode fazer para se manter na linha reta seria apontar na direção contrária a corrente () e manter sua rapidez máxima. Mas nesse caso ele simplesmente ficaria parado em relação ao solo, isso porque a soma vetorial:
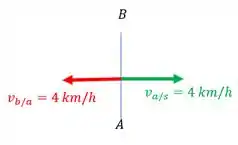
Daria para o vetor velocidade em relação ao solo, porque teríamos uma soma de vetores iguais e opostos
Passo 3
Para melhorar a visualização, a gente pode pensar num ângulo para , por exemplo, o da letra b. Olha como ficaria a soma vetorial usando o método do paralelogramo
não fica na direção AB. Quanto mais próximo é de , mais próximo esse vetor ficaria de AB, mas também, quanto mais próximo de AB, menor é o vetor. De modo que em , o vetor é zero.
Em outras palavras, nesse caso é impossível atravessar o rio sobre a linha reta , e o melhor a fazer é desistir.
Resposta
Letra (d).