Um satélite orbita o Sol com período de translação de 1,0 dia. Qual é o raio da órbita?

Vamos analisar o movimento do satélite em torno do Sol:

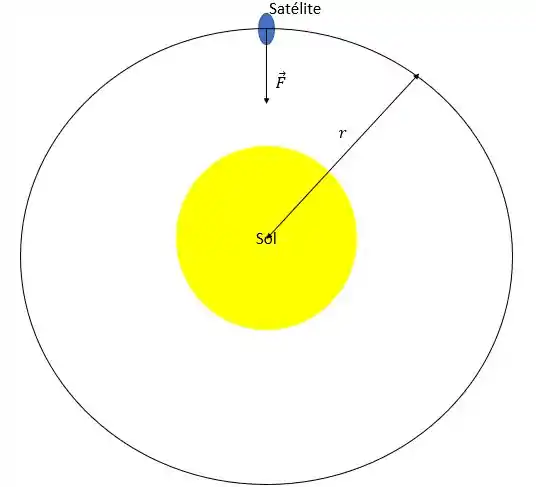
Sabemos que o satélite fica orbitando o Sol, que vai exercer uma força gravitacional sobre o satélite. O módulo dessa força é:

Onde é a massa do Sol, é a massa do satélite, é a constante gravitacional e é a distância entre o Sol e o satélite.

Como o satélite fará uma trajetória circular em torno do Sol, acaba sendo o raio dessa trajetória.

Da mesma forma, como estamos em um movimento circular, temos uma força que vai desempenhar o papel de força centrípeta, que aponta para o centro da trajetória. Nesse caso, a única força que aponta para o centro da trajetória é a força gravitacional, logo ela será a nossa força centrípeta!!

A força centrípeta é dada por , onde é a massa da partícula e é a velocidade. Nesse caso, então, teremos:

Mas também sabemos que , onde é o período da trajetória, dado no enunciado como . Assim:

Podemos cortar e arrumar a fração:

Isolando :

Assim:

Fazendo essa conta: