Exercícios de Velocidade e Período Orbital - Lista de Exercícios Resolvida

Qual deve ser a velocidade orbital de um satélite que descreve uma órbita circular a acima da superfície terrestre?

Dados:

Constante gravitação:

Massa da Terra:

Raio da Terra:

Um satélite, com uma massa de , se move em uma órbita circular acima da superfície da Terra. (a) Qual é a força gravitacional sobre o satélite? (b) Qual é a rapidez do satélite? (c) Qual é o período do satélite?

Dados:

Um ônibus espacial numa órbita de 300km de altura ( quer capturar um satélite menor para efetuar reparos. Quais são os valores de velocidade do ônibus e do satélite nesta órbita?

Dados:

- Massa da Terra:

- Raio da Terra:

- Constante Gravitação:

Centenas de milhares de asteroides giram em torno do Sol no interior do cinturão de asteroides, que se estende desde uma distância do Sol de até cerca de . a) Ache o período orbital (em anos) para i) um asteroide na parte interna do cinturão e ii) um asteroide na parte externa do cinturão. Considere órbitas circulares.

Dados:

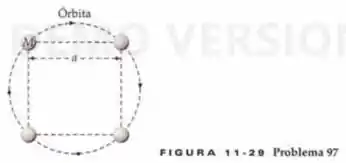
Quatro planetas idênticos formam um quadrado, como mostrado na Figura 11-29. Se a massa de cada planeta é e o lado do quadrado tem comprimento , qual deve ser a rapidez de cada planeta, se eles devem permanecer em órbita em torno de seu centro comum, sob a influência de suas atrações mútuas?

Dois satélites orbitam em torno de um planeta que tem distribuição esfericamente simétrica de massa. Cada um está sujeito apenas à força gravitacional do planeta, descrevendo movimentos circulares uniformes. Se o primeiro satélite tem velocidade em uma órbita de raio e o segundo velocidade , então o raio da órbita do segundo satélite é

(a)

(b)

(c)

(d)

(e)

Dois satélites orbitam em torno de um planeta que tem distribuição esfericamente simétrica de massa. Cada um está sujeito apenas à força gravitacional do planeta, descrevendo movimentos circulares uniformes. Se o primeiro satélite tem velocidade em uma órbita de raio e o segundo velocidade , então o raio da órbita do segundo satélite é

(a)

(b)

(c)

(d)

(e)

Uma nave espacial com massa se encontra em uma órbita circular acima da superfície da Lua. Ela necessita passar para uma órbita circular acima da superfície. Quanto trabalho os foguetes da nave terão que realizar?

Dados:

Constante gravitacional:

Massa da Lua:

Raio da Lua:

O satélite 1 está em uma certa órbita circular em torno de um planeta, enquanto o satélite 2 está em uma órbita circular de raio maior em torno do mesmo planeta. Considere as seguintes afirmações:

1) O satélite 2 tem o maior período.

2) O satélite 2 tem o menor período.

3) O satélite 1 tem a maior velocidade.

4) O satélite 1 tem a menor velocidade.

5) Os dois satélites têm o mesmo período e a mesma velocidade.

A(s) informação(ões) correta(s) é(são):

a) e ;

b) e ;

c) e ;

d) ;

e) e ;

No topo de uma montanha na Lua, um projétil é disparado horizontalmente com a velocidade (velocidade de escape),onde é a distância do topo da montanha ao centro da Lua, é a massa da Lua e é a constante de gravitação universal. Neste caso, desconsiderando a contribuição da Terra e do Sol para o campo gravitacional, o qual a curva que descreve a trajetória do objeto?

a) Uma parábola ou uma hipérbole, se afastando da Lua.

b) Uma parábola, caindo na superfície da Lua.

c) Uma elipse.

d) Um círculo.

e) Uma reta.

Qual é a velocidade orbital de um cubo de gelo nos anéis de Saturno, se a massa de Saturno é e o raio médio dos anéis é de ?

(Dado: )

(A)

(B)

(C)

(D)

(E)

Qual deve ser a velocidade orbital de um satélite que descreve uma órbita circular acima da superfície terrestre?

Resposta: 7,47 km/s

Dados:

Constante gravitacional:

Raio da Terra:

Massa da Terra:

Considere as oscilações de um pêndulo e de um sistema massa-mola disposto na vertical na superfície da Terra, com períodos e , respectivamente. Suponha que e são os períodos de oscilação dos mesmos objetos para experimentos realizados na Lua. É correto afirmar que:

(A) e

(B) e

(C) e

(D) e

(E) e

Satélites são ditos geoestacionários (ou geossincrônicos) quando executam uma órbita circular equatorial em torno da Terra com período de 24h. Isto é, o período do satélite é igual ao período de rotação da Terra. Para um observador no equador da Terra, o satélite comporta-se como se estivesse estacionário num local fixo no céu. Qual afirmação é verdadeira para um satélite em tal órbita?

(A) Não há força gravitacional agindo no satélite.

(B) O satélite não está sujeito a nenhuma aceleração.

(C) Só existe um raio que permite uma órbita geoestacionária.

(D) Existe uma força tangencial que ajuda o satélite a acompanhar a rotação da Terra.

(E) A força gravitacional é equilibrada por uma força que aponta para longe do centro da Terra.

Considere um satélite artificial em órbita circular em torno da Terra. Diga como as seguintes propriedades do satélite variam em função do raio de sua órbita:

a) módulo da velocidade;

b) energia cinética;

c) momento angular;

d) período.

O planeta Vênus demora 225 dias para completar uma órbita em torno do Sol, em uma trajetória praticamente circular. Sabendo que a massa do Sol é M = 1,99 x Kg, o raio da órbita de Vênus é aproximadamente: Considere G = 6,67 x N.m2 /kg2

a) 2,0 x m

b) 1,0 x m

c) 19 x m

d) 2,0 x m

e) 1,1 x m

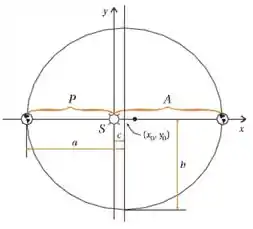
Os planetas giram em torno do sol em órbitas elípticas com o sol em um dos focos (veja a figura). Este princípio foi determinado por Kepler e publicado em sua obra Astronomia Nova - De Motibus Stellae Martis em 1609. (Veja na página seguinte a capa do trabalho).

A excentricidade e de uma elipse é definida como sendo a razão entre as distâncias c (distância de um foco ao centro da cônica) e a (distância do centro da cônica ao semi-eixo maior).

Observe na tabela para dados astronômicos que os planetas Vênus e Netuno possuem excentricidades muito baixas e portanto são planetas que descrevem órbitas aproximadamente circulares em torno do sol. Com base nestas informações, determine a frequência angular orbital do planeta Vênus em torno do sol em radianos por segundo.