Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Exercício - Ex. 45
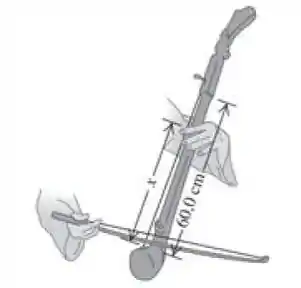
O segmento de uma corda de certo instrumento entre a ponte de apoio das cordas e a extremidade superior (a parte que vibra livremente) possui comprimento igual a e massa igual a . Quando tocada, a corda emite a nota .
- Em que ponto o violoncelista deve colocar o dedo (ou seja, qual é a distância entre o ponto e a ponte de apoio das cordas) para produzir uma nota Nas duas notas e a corda vibra no modo fundamental.
- Sem afinar novamente, é possível produzir uma nota nessa corda? Justifique sua resposta.
Passo 1
Letra a)
Olá tudo bem? Vamos começar?
Com a frequência de e o compriemento da corda, podemos encontrar a velocidade das ondas na corda. No modo fundamental , então o comprimento de onda é igual a . Assim a velocidade é:
Passo 2
Mas queremos saber a posição para obtermos . Então fazemos , e o novo comprimento de onda é:
E como sabemos que ambas notas vibram no modo fundamental, então:
Passo 3
Letra b)
Como não há uma nova afinação, a velocidade da onda é conservada. Sendo assim, queremos saber o novo comprimento de onda para a frequência de .
Da expressão temos:
E lembrando de novo que as notas vibram no modo fundamental, o valor de é:
Beleza? Vamos pra próxima?