Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.Problemas Adicionais - Ex. 81a

Em um sistema estelar binário, duas estrelas de massa 3,0   .   10 30   k g giram em torno do centro de massa do sistema a uma distância de 1,0   .   10 11   m . (a) Qual é a velocidade angular das estrelas em relação ao centro de massa? (b) Se um meteorito passa pelo centro de massa do sistema perpendicularmente ao plano de órbita, qual a menor velocidade que o meteorito deve ter ao passar pelo centro de massa para poder escapar para o “infinito” depois de passar pelo sistema binário?

Passo 1

Vamos lembrar que em um sistema estelar binário as duas estrelas orbitam o centro de massa do sistema:

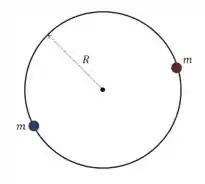
Se pensarmos em uma dessas estrelas, podemos escrever as forças sobre ela:

F g = G m 2 2 R 2 = G m 2 4 R 2

Como essas forças mantém a estrela em uma trajetória circular, podemos toma-la como uma força centrípeta:

G m 2 4 R 2 = m v 2 R

Cortando o que for possível:

v 2 = G m 4 R

Passo 2

A questão pediu a resposta em termos da velocidade angular ω , cuja relação com a velocidade linear é:

v = ω R

Substituindo isso na fórmula:

ω R 2 = G m 4 R

ω = G m 4 R 3 = 6,67.10 - 11 3.10 30 4 10 11 3 = 2,2   .   10 - 7   r a d / s

E essa é a resposta da letra (a).

Resposta

(a) ω =   2,2   .   10 - 7   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um planeta leva 300 dias (terrestres) para completar uma órbita circular em torno do seu sol, que tem uma massa de 6,0 × 10 30k g . Quais são (a) o raio da órbita e (b) a velocidade orbital do planeta
12.32. Planeta Vulcano. Suponha que houvesse sido descoberto um planeta entre o Sol e Mercúrio, com uma órbita circular de raio igual a 2/3 do raio orbital de Mercúrio. Qual seria o período orbital de
12.37. A espaçonave Helios B possuía uma velocidade de 71 km/s quando ela estava a 4,3 ⋅ 10 7k m do Sol. a) Prove que ela não estava em uma órbita circular em torno do Sol. b) Prove que sua órbita em
12.35. a) Use a Figura 12.19 para mostrar que a distância entre o Sol e um planeta no periélio é igual a 1 ⋅ e a , e a distância entre o Sol e um planeta no afélio é igual a 1 + e a e, portanto, a som
12.34. Em março de 2006, foram descobertos dois pequenos satélites orbitando Plutão, um deles a uma distância de 48000 km e o outro a 64000 km. Já se sabia que Plutão possuía um grande satélite, Caron