Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Problemas - Ex. 77
Superposição de ondas estacionárias. A corda de uma guitarra de comprimento L é puxada de tal modo que a onda resultante é a soma do modo fundamental com o segundo harmônico. Ou seja, a onda resultante é dada por
Onde
Com e .
a) Para que valores de ocorrem os nós de ?
b) Para que valores de ocorrem os nós de ?
c) Faça um gráfico da onda resultante para , , , e .
d) A soma das duas ondas produz uma onda estacionária? Explique
Passo 1
Como estamos considerando ondas estacionárias, temos que os locais onde existem nós não mudaram ao longo do tempo.
Nossa corda de guitarra está fixada em ambas as extremidades logo as extremidades são nós para todos os harmônicos.
O modo fundamental possui apenas dois nós, já o segundo harmônico possui um nó a mais.
Passo 2
a) Como representa o primeiro harmônico temos que seus nós serão as extremidades, desta forma eles estão em e .
Passo 3
b) Como representa o segundo harmônico temos que seus nós serão as extremidades e o centro, desta forma eles estão em , e .
Passo 4
c) Para montar esses gráficos basta substituir o tempo em e variar . Lembrando que são constantes.
Gráfico para :
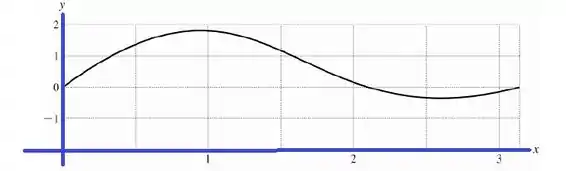
Gráfico para :
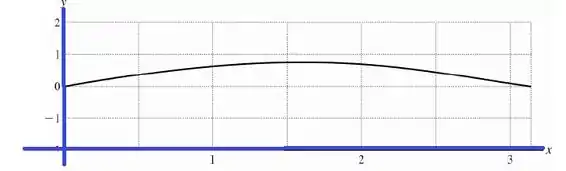
Gráfico para :
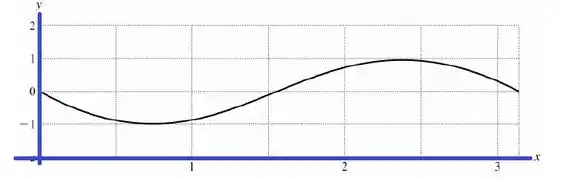
Gráfico para :
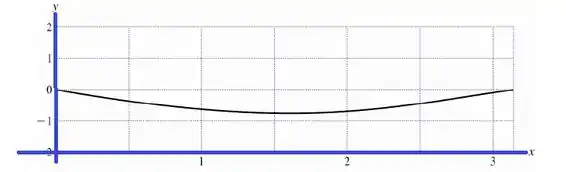
Gráfico para :
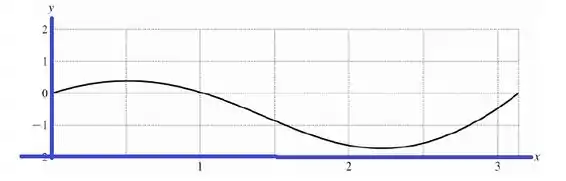
Passo 5
d) Observando os gráficos do item (c) que são feitos a partir da soma de duas ondas , mostram que as localizações dos nós e dos antinós estão variando com o tempo, logo temos que a soma de duas ondas estacionárias com frequências diferentes não é uma onda estacionária.
Resposta
Ei, a resposta está no passo a passo :)