Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 38.6 - Ex. 66

Suponha que A = B = ψ 0 na Eq. 38-18. Nesse caso, a equação representa a soma de duas ondas de matéria de mesma amplitude, propagando-se em sentidos opostos. (a) Mostre que, para esses valores de A e B , Ψ x , t 2 é dado por

Ψ x , t 2 = 2 ψ 0 2 1 + cos ⁡ 2 k x

(b) Plote essa função e mostre que representa o quadrado da amplitude de uma onda estacionária. (c) Mostre que os nós da onda estacionária estão situados nos pontos para os quais

x = 2 n + 1 λ 4 ,             o n d e         n = 0 ,   1 ,   2 ,   3 ,   …

e λ é o comprimento de onda de de Broglie da partícula. (d) Escreve uma expressão do mesmo tipo para as posições mais prováveis da partícula.

Passo 1

Da equação 38-18, temos que

Ψ x , t = A e i ( k x - ω t ) + B e - i ( k x + ω t )

Fazendo A = B = ψ 0 :

Ψ x , t = ψ 0   e - i ω t   e i k x + e - i k x

Assim, tomando o complexo conjungado:

Ψ * x , t = ψ 0 e i ω t   e - i k x + e i k x

Portanto,

Ψ x , t 2 = ψ 0   e - i ω t   e i k x + e - i k x ⋅ ψ 0 e i ω t   e - i k x + e i k x

Logo,

Ψ x , t 2 = ψ 0 2 1 + e 2 i k x + e - 2 i k x + 1 = ψ 0 2   2 + e 2 i k x + e - 2 i k x

Sabemos também que

e i θ = cos ⁡ θ + i   s e n   θ               e             e - i θ = cos ⁡ θ - i   s e n   θ

Portanto,

e i θ + e - i θ = 2 cos ⁡ θ

Logo,

e 2 i k x + e - 2 i k x = 2 cos ⁡ 2 k x

Desta forma,

Ψ x , t 2 = ψ 0 2 2 + 2 cos ⁡ 2 k x = 2 ψ 0 2 1 + cos ⁡ 2 k x

O gráfico de Ψ x , t 2 é

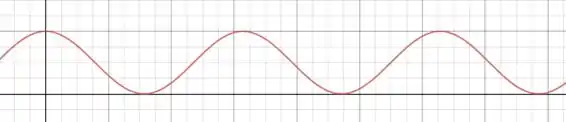
Passo 2

Vamos lembrar também que

cos ⁡ 2 θ = cos 2 ⁡ θ - s e n 2 θ = 2 cos 2 ⁡ θ - 1 ⇒ 1 + cos ⁡ 2 θ = 2 cos 2 ⁡ θ

Portanto,

Ψ x , t 2 = 2 ψ 0 2 ⋅ 2 cos 2 ⁡ k x = 2 ψ 0 cos ⁡ k x 2

A função densidade de probabilidade representa o quadrado da amplitude de uma onda estacionária!

Passo 3

Os nós da onda estacionária ocorrem onde Ψ x , t 2 = 0 :

cos ⁡ k x = 0 ⇒ k x = π 2 + n π

Por outro lado, temos que

k = 2 π λ

Assim,

2 π x λ = π 1 2 + n ⇒ x = λ 2 1 2 + n = 2 n + 1 λ 4

Passo 4

Por fim, queremos achar as posições mais prováveis, que ocorrem quando a densidade de probabilidade Ψ x , t 2 for máxima. Assim,

cos ⁡ k x = ± 1

Devemos considerar tanto o sinal positivo como negativo pois o cosseno é elavado ao quadrado! Assim,

k x = n π ⇒ 2 π x λ = n π

Portanto,

x = n λ 2

Resposta

Demonstração.

x = n λ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você está participando de uma competição no qual os jogadores deixam cair bolas de gude de 20,0 g do alto de um edifício para atingir um pequeno alvo situado a 25,0 m abaixo. Com base no princípio de
Um estudante universitário propôs a seguinte expressão para a função de onda de uma partícula livre de massa m (uma partícula para qual a função energia potencial U ( x ) é igual a zero): Ψ ( x ) = e
Exercício de Livro
Exercício de Livro
Exercício de Livro