Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 10.Problemas - Ex. 76

Tarzan meteu-se em uma briga com os animais e mais uma vez precisou ser resgatado por Jane. Jane, com 60,0 kg, parte do repouso em uma altura de 5,00 m nas árvores e balança até o solo usando um cipó fino, porém muito rígido, com 30,0 kg e 8,00 m de comprimento. Ela chega no momento exato de agarrar Tarzan, com 72,0 kg, das garras de um hipopótamo zangado. Qual é a velocidade angular de Jane (e do cipó) (a) imediatamente antes de agarrar Tarzan e (b) imediatamente depois que o agarra? (c) Até que altura Tarzan e Jane subirão em seu primeiro balanço depois do resgate audacioso?

Passo 1

E aiiiiiiiii galera, tudo bom com vocês?

Vamos fazer mais uma questão!!

Letra a:

As posições inicial e final de Jane e do cipó para o primeiro estágio são esboçados na figura a. A altura inicial do centro do cipó é h cipó 1 = 6.50 m e sua altura final é h cipó 2 = 4.00 m .

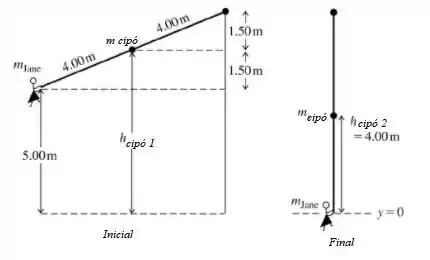
A conservação de energia nos dá:

U 1 + K 1 = U 2 + K 2

K 1 = 0

Então,

m J a n e g 5.00 m + m c i p ó g 6.50 m

m cipó   g ( 4.00 m ) + 1 2 I tot  ω 2

ω = m J a n e ( 5.00 m ) + m c i p ó ( 250 m ) g 1 3 m c i p ó + m J a n e l 2

ω = 2 [ ( 60.0 k g ) ( 5.00 m ) + ( 30.0 k g ) ( 250 m ) ] 9.80 m / s 2 1 3 ( 30.0 k g ) + 60.0 k g ( 8.00 m ) 2 = 128 r a d / s

Passo 2

Letra b:

Como a conservação do momento angular aplicada à colisão, temos L 1 = L 2 ,   então   I 1 ω 1 = I 2 ω 2 .

a 1 = 1.28 r a d / s I 1 = 1 3 30.0 k g + 60.0 k g ( 8.00 m ) 2 = 4.48 × 10 3 k g ⋅ m 2 I 2 = I 1 + m Tarzan   l 2 = 4.48 × 10 3 k g ⋅ m 2 + ( 72.0 k g ) ( 8.00 m ) 2 = 9.09 × 10 3 k g ⋅ m 2 a 2 = I 1 I 2 ω 1 = 4.48 × 10 3 k g ⋅ m 2 9.09 × 10 3 k g ⋅ m 2 ( 1.28 r a d / s ) = 0.631 r a d / s

Passo 3

Letra c:

A posição final de Tarzan e Jane, quando eles atingem sua altura máxima, é mostrada na figura:

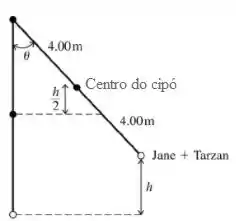
Se Tarzan e Jane sobem para uma altura h, então o centro do cipó sobe para uma altura h/2.

Pela conservação de energia temos:

1 2 I ω 2 = m Jane  + m Tarzan  g h + m cipó g h / 2

Onde, I = 9.09 × 10 3 k g ⋅ m 2 e ω = 0.631 r a d / s , da parte b

h = I ω 2 2 m Jane  + m Tarzan  + 0.5 m cipó   g = 9.09 × 10 3 k g ⋅ m 2 ( 0.631 r a d / s ) 2 2 60.0 k g + 72.0 k g + 15.0 k g 9.80 m s 2 = 1.26 m

Resposta

  1. 128 r a d s
  2. 0.631 r a d / s
  3. 1.26 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma estação espacial é construída no formato de um anel oco de massa 5,00 × 10 4k g . Os membros da equipe caminham por um deque formado pela superfície interna da parede cilíndrica externa do anel, c
Um disco com momento de inércia I 1 gira em torno de um eixo vertical e sem atrito com velocidade angular w i . Um segundo disco, com momento de inércia I 2 e inicialmente parado, cai sobre o primeiro
O disco na Figura 10.25 tem massa de 0,120k g . A distância dele do centro de rotação é originalmente 40,0c m , e ele está deslizando com uma velocidade de 80,0c m / s . O fio é puxado para baixo a 15
Uma mulher de 60,0k g em pé na borda ocidental de um prato giratório tem momento de inércia de 500k g⋅m 2 e um raio de 2,00m . O prato giratório está inicialmente em repouso e livre para girar sem atr
Por que a seguinte situação é impossível? Uma estação espacial com o formato de uma roda-gigante tem raio de r=100m e momento de inércia de 5,00 × 10 8k g⋅m 2 . Uma equipe de 150 pessoas de massa médi