Um trenó pesando 200 N é mantido em posição, sobre plano inclinado de , pelo atrito estático. O coeficiente de atrito estático entre o trenó e o plano inclinado é 0,50. (a) Qual é a magnitude da força normal sobre o trenó? (b) Qual é a magnitude da força de atrito estático sobre o trenó? (c) Agora, o trenó é puxado rampa acima (figura acima) com rapidez constante por uma criança que sobe a rampa à frente do trenó. A criança pesa 500 N e puxa a corda com uma força constante de 100 N. A corda forma um ângulo de com o plano inclinado e tem massa desprezível. (d) Qual é a magnitude da força de atrito cinético sobre o trenó? (e) Qual é a magnitude da força exercida sobre a criança pelo plano inclinado?
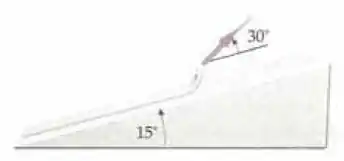
Passo 1
Letra (a)
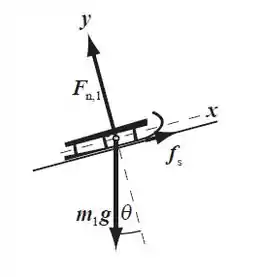
Segunda lei de Newton em y:
Agora joga os valores dados:
Passo 2
Letra (b)
Agora faz a segunda lei de Newton em x:
Joga os valores de novo:
Passo 3
Letra (c)
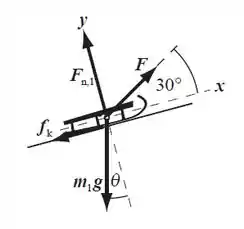
Segunda lei de Newton de novo, em x:
Isola o :
Agora substitui os valores:
Passo 4
Letra (d)
O coeficiente de atrito cinético vem da fórmula:
Agora a gente faz o que? Isso mesmo, segunda lei de Newton, em y:
Isola a força normal:
Pega a (2) e joga em (1):
E agora joga os valores:
Passo 5
Letra (e)
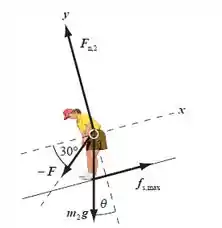
A força que o plano inclinado faz na criança é a soma da normal com a força de atrito, então:
Para achar as duas, vamos usar a segunda lei de Newton em x e em y para a criança:
Jogando os valores:
Passo 6
Agora a força normal:
Jogando valores de novo:
Agora joga os valores achados em (3):
Resposta
Letra (a): 190 N
Letra (b): 52 N
Letra (c): 35 N
Letra (d): 0,24
Letra (e): 580 N