Três estrelas, cada uma com a massa do Sol, formam um triângulo equilátero com lados de . (Este triângulo se encaixaria com precisão na órbita de Júpiter). O triângulo precisa girar, pois, do contrário, as estrelas colidiriam no centro. Qual é o período de rotação? Expresse sua resposta em anos.
Dados:
Massa do sol:
Constante gravitacional universal:
Passo 1
Uma ilustração pode ajudar a gente a entender melhor a situação:
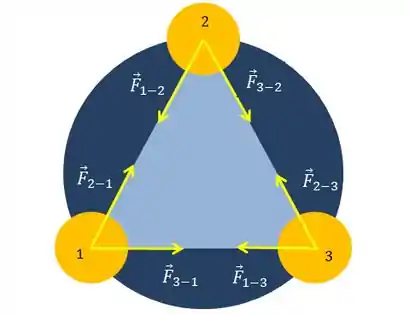
Essas no desenho são as forças gravitacionais que cada estrela “sofre” e “exerce”. Mas, como diz o enunciado, o conjunto das estrelas precisa rotacionar, pois do contrário elas colidiriam no centro do triângulo.
Se a gente decompõe essas forças em suas componentes radial e tangencial, você vai ver que vamos chegar a uma força resultante centrípeta, que é a causadora da rotação do conjunto das estrelas.
Considerando as estrelas todas idênticas entre si, o trabalho que fazemos pra uma delas vale exatamente igual pras outras, certo? Decompondo as duas forças que agem na estrela nas componentes tangencial e radial, temos os seguintes esquemas:

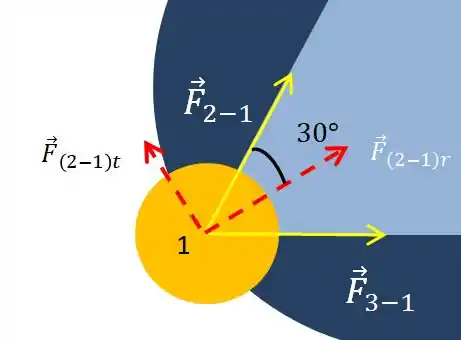
Se você reparar, as componentes tangenciais e , de mesmo módulo, direção mas sentidos diferentes, se anulam.
Assim, a força resultante derivada das forças gravitacionais é uma força centrípeta (que aponta pro centro), que equivale ao somatório das forças e .
Agora, a gente precisa determinar o módulo dessas duas forças, e dá pra fazer isso analisando os seguintes triângulos retângulos que existem nas figuras acima:
Passo 2
Agora, a gente precisa determinar o módulo dessas duas forças, e e dá pra fazer isso analisando os seguintes triângulos retângulos que existem nas figuras acima:

A gente pode escrever a seguinte relação trigonométrica:
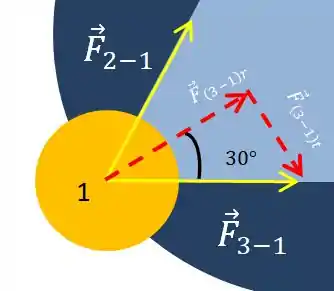
Fazemos o mesmo agora:
No fim das contas, elas têm o mesmo módulo, e isso já era de se esperar, pois estamos trabalhando dentro de um triângulo equilátero e com estrelas idênticas.
Passo 3
Como já concluímos, o módulo força resultante, centrípeta, causadora do movimento circular das estrelas, é a soma dos módulos das forças e . Escrevemos isso:
Substituímos pelas expressões que achamos pra essas forças:
Podemos colocar em evidência e escrever:
Certo, agora já podemos escrever algumas coisas que já sabemos. O módulo da força centrípeta vale:
Onde é a velocidade da rotação do triângulo (translação das estrelas) e é o raio da órbita
E o módulo da forças gravitacionais e valem:
Onde é o tamanho do lado do triângulo equilátero, que é a distância entre as estrelas.
Por fim, a gente vai poder escrever o seguinte:
Simplificando, teremos:
Passo 4
Antes de a gente continuar trabalhando nessa última equação, a gente precisa correlacionar o raio da órbita com o lado do triângulo equilátero. Vamos fazer isso também com trigonometria. Olha só:

Escrevemos:
Agora, voltamos a trabalhar naquela equação a que chegamos, substituindo por .
Passo 5
Vamos ter:
Simplificamos o que for possível:
E, assim, chegamos a uma expressão pra velocidade orbital!
Passo 6
Agora você vai ver que, com essa expressão pra velocidade orbital , conseguimos uma expressão pro período orbital .
Lá da cinemática, você sabe que a velocidade de um corpo nada mais é que a distância que ele percorre sobre o tempo , levado pra percorrê-la, certo? Assim:
Pro nosso caso, de uma volta completa pela órbita circular (uma rotação do triângulo), essa distância equivale ao comprimento da circunferência da órbita: ; o tempo pra isso acontecer vale (período), assim, .
Temos assim, a seguinte expressão pra velocidade orbital:
Como queremos o período de rotação do triângulo (translação das estrelas), isolamos e obtemos:
Aqui, lembre-se, . Assim:
Passo 7
Basta agora aplicarmos os valores que temos na expressão e determinar o período. Vamos ter:
Jogamos isso na calculadora e teremos no final:
Passo 8
Nos foi pedido o período de rotação do triângulo em anos. Pra isso, consideramos um ano de 365 dias.
Sabe-se que 1 dia tem 86400 segundos. Assim, quantos segundos temos em um ano de 365 dias?
Agora, dividimos o período em segundos pela quantidade de segundos que há em 1 ano e vamos determinar :