Um tubo cilíndrico cuja secção transversal tem área está dobrado em forma de , com um ramo vertical e o outro formando um ângulo com a vertical, e contém uma massa de líquido de densidade . Produz-se um pequeno desnível entre um ramo e outo. Calcule a frequência angular de oscilação da massa líquida.
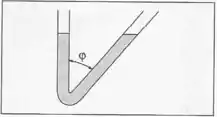
Passo 1
Imagine uma pequena coluna de líquido, do lado esquerdo do tubo, com altura . A massa dessa coluna é:
Se você pressionar essa coluna para baixo do lado esquerdo, a mesma quantidade de água vai subir do lado direito:
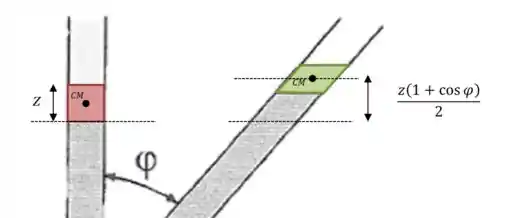
Passo 2
Vamos procurar uma expressão para a energia total do sistema durante esse deslocamento:
Para a energia cinética, temos:
Onde é a massa total do líquido. Para a energia potencia vamos considerar o deslocamento da nossa massa :
Onde é posição do da massa deslocada, conforme representamos no desenho:
Então a energia total é:
Passo 3
Pela lei de conservação de energia, temos que:
Não esqueça de aplicar a regra da cadeia para derivar e em relação ao tempo:
Dividindo os dois lados por :
Que é a equação de um oscilador harmônico com a seguinte frequência angular:
Resposta
A frequência angular é .