Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 75

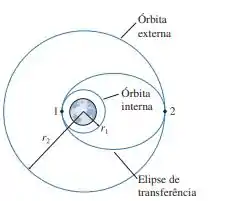
Vamos analisar com mais detalhe como um satélite é transferido de uma órbita circular para outra. A FIGURA PD13.75 mostra duas órbitas circulares, de raios r1 e r2, e uma órbita elíptica que as conecta. Os pontos 1 e 2 estão nas extremidades do semi-eixo maior da elipse.

a. Um satélite que descreve uma órbita elíptica precisa satisfazer a duas leis de conservação. Utilize essas duas leis para provar que as velocidades dos pontos 1 e 2 são dadas pelas relações.

v 1 ' = 2 G M ( r 2 / r 1 ) r 1 + r 2                                     v 2 ' = 2 G M ( r 1 / r 2 ) r 1 + r 2

Os apóstrofos usados indicam que essas são as velocidades na órbita elíptica. As duas se reduzem à Equação 13.22 se r 1 = r 2 = r .

b. Considere um satélite de comunicação que precisa ser impulsionado de uma órbita 300 km acima da Terra para uma órbita geossíncrona, a 35.900 km de altitude. Determine a velocidade v 1 na órbita circular interna e a velocidade v 1 no ponto baixo da órbita elíptica que conecta as duas órbitas circulares.

c. Quanto trabalho deve ser realizado pelo motor do foguete para transferir o satélite da órbita circular para a órbita elíptica?

d. Agora encontre a velocidade v 2 no ponto mais alto da órbita elíptica e a velocidade v 2 na órbita circular externa.

e. Quanto trabalho deve ser realizado pelo motor do foguete para transferir o satélite da órbita elíptica para a órbita circular externa?

f. Calcule o total de trabalho realizado e compare suas respostas com o resultado do Exemplo 13.6.

Passo 1

Aqui temos um problema em que devemos saber equacionar órbitas circulares e órbitas elípticas. No geral, é bem mais fácil trabalhar com órbitas circulares, pois a velocidade é a mesma em todos os pontos da órbita e é dada por:

v = G M r

onde G é a constante gravitacional, M é a massa do planeta e r a distância até o centro do planeta.

Órbitas elípticas são um pouco mais complicadas. Há duas grandezas que permanecem inalteradas durante todo o movimento do satélite: i) o momento angular; ii) a energia mecânica. O momento angular é conservado pois a força gravitacional é uma força central: ela sempre aponta para o centro do planeta; a energia mecânica é conservada pois a força gravitacional é uma força conservativa. Ok, vamos lá.

Passo 2

  1. Há duas conservações que devemos levar em conta:
    1. A conservação do momento angular:

      2. m r 1 v 1 ' = m r 2 v 2 ' ∴ v 2 ' = r 1 r 2 v 1 '

    2. A conservação da energia mecânica:

    E a f é l i o = E p e r i é l i o - G m M r 2 + 1 2 m v 2 ' 2 = - G m M r 1 + 1 2 m v 1 ' 2 G M 1 r 1 - 1 r 2 = 1 2 v 1 ' 2 - v 2 ' 2 2 G M r 2 - r 1 r 1 r 2 = v 1 ' 2 1 - r 1 2 r 2 2 2 G M r 2 - r 1 r 1 r 2 = v 1 ' 2 r 2 2 - r 1 2 r 2 2 2 G M r 2 - r 1 r 1 = v 1 ' 2 r 2 - r 1 r 2 + r 1 r 2 v 1 ' = 2 G M r 2 r 1 r 1 + r 2

    Também, como v 2 ' = r 1 r 2 v 1 ' , segue que

    v 2 ' = 2 G M r 1 r 2 r 1 + r 2

    como queríamos provar.

    Passo 3

  2. Para a órbita circular

    3. v 1 = G M r v 1 = 6,67 × 10 - 11 5,98 × 10 24 6,37 × 10 6 + 3 × 10 5 v 1 = 7730   m / s

    Para a órbita elíptica, basta usar a equação de v 1 ' , com r 1 = 6370 + 300   k m e r 2 = 6370 + 35.900   k m :

    v 1 ' = 2 G M r 2 r 1 r 1 + r 2 v 1 ' = 2 6,67 × 10 - 11 5,98 × 10 24 42,3 × 10 6 6,67 × 10 6 48,94 × 10 6 v 1 ' = 10.160   m / s

    Passo 4

  3. O trabalho será igual a variação de energia cinética (teorema da energia cinética). Logo,

    4. W 1 = Δ E c W 1 = m 2 v 1 ' 2 - v 1 2 Note que não nos foi fornecido a massa do satélite! Sendo assim, fica impossível de se determinar o trabalho. Porém, a ideia usada é essa ai.

    Passo 5

  4. Mesmo procedimento do item b.

    5. v 2 = G M r v 2 = 6,67 × 10 - 11 5,98 × 10 24 42,3 × 10 6 v 2 = 3070 m s

    Para a elíptica, podemos aplicar a fórmula para v 2 ' :

    v 2 ' = 2 G M r 1 r 2 r 1 + r 2 v 2 ' = 2 6,67 × 10 - 11 5,98 × 10 24 6,67 × 10 6 42,3 × 10 6 48,94 × 10 6 v 2 ' = 1600   m / s

    Passo 6

  5. O trabalho será dado por:

    6. W 2 = Δ E c W 2 = m 2 v 2 2 - v 2 ' 2

    Novamente, não podemos determinar o trabalho, pois a massa m não foi dada.

    Passo 7

  6. O trabalho total será obtido somando W 1 + W 2 .

Resposta

  1. Demonstração.
  2. 7730 m/s e 10.160 m/s.
  3. m 2 v 1 ' 2 - v 1 (não nos foi dado a massa m)
  4. 3070 m/s e 1600 m/s.
  5. m 2 v 2 - v 2 ' 2
  6. W 1 + W 2 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma forma de atacar um satélite em órbita da Terra é disparar uma saraivada de projéteis na mesma órbita do satélite, no sentido oposto. Suponha que um satélite em órbita circular, 500k m acima da sup
Na figura, dois satélites, A e B , ambos de massa m = 125k g , ocupam a mesma órbita circular de raio r = 7,87.10 6m em torno da Terra e se movem em sentidos opostos, estando, portanto, em rota de col
(a) A que distância da superfície da Terra a energia necessária para fazer um satélite subir até essa altitude é igual à energia cinética necessária para que o satélite se mantenha em órbita circular
Dois satélites, A e B , ambos de massa m , estão em órbita circular em torno da Terra. O satélite A orbita a uma altitude de 6370k m e o satélite B a uma altitude de 19.110k m . O raio da Terra é 6370
Uma certa estrela de nêutrons tem uma massa igual à do Sol e um raio de 10k m . (a) Qual é a aceleração da gravidade na superfície da estrela? (b) Com que velocidade um objeto estaria se movendo se ca