Você está projetando uma sequência de viagem em cipó, para o último filme de Tarzan. Para determinar a rapidez do Tarzan no ponto mais baixo de sua trajetória, para se certificar de que ela não ultrapassa os limites estabelecidos de segurança, você elabora um modelo em que o sistema Tarzan+cipó é um péndulo. Em seu modelo, a partícula (Tarzan, 100 kg de massa) oscila na extremidade de um fio leve (o cipó) de comprimento preso a um suporte. O ângulo entre a vertical e o fio é . (a) Desenhe um diagrama de corpo livre para o corpo na extremidade do fio (Tarzan no cipó). (b) Uma distância infinitesimal ao longo do arco (pelo qual o corpo se move) é . Escreva uma expressão para o trabalho total realizado sobre a partícula enquanto ela percorre esta distância, para um ângulo arbitrário . (c) Se = 7,0 m e se a partícula parte do repouso a um ângulo de 50º, determine a energia cinética da partícula e sua rapidez, no ponto mais baixo do percurso, usando o teorema do trabalho-energia cinética.
Passo 1
Letra (a)
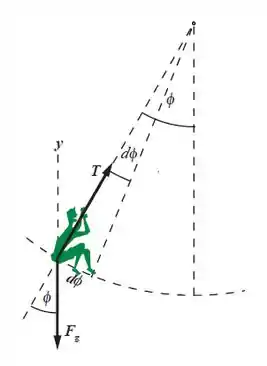
Passo 2
Letra (b)
O trabalho de uma força é dado pela fórmula:
Podemos usar essa fórmula quando a força é constante e quando o deslocamento d é muito pequeno, que é o caso. A tração é sempre perpendicular ao deslocamento, então só a força gravitacional exerce trabalho:
Só que
O sinal de menos é porque o ângulo está diminuindo.
Como :
Passo 3
Letra (c)
Usando o teorema trabalho-energia, vamos ter o seguinte:
Lembrando que a energia cinética inicial é nula, pois parte do respouso:
Passo 4
O trabalho nesse percurso é dado pela integral:
Jogando os valores:
Passo 5
Voltando para a fórmula :
Isolando o :
Jogando os valores:
Resposta
Letra (a):
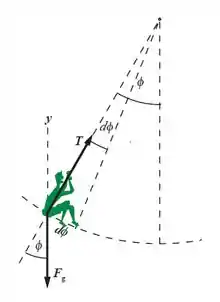
Letra (b):
Letra (c): 7,0 m/s