Você projetou uma portinhola para gato, feita de um pedaço quadrado de madeira compensada de de espessura e de lado, articulada em cima. Para que o gato tenha tempo suficiente para atravessar a portinhola com segurança, ela deve ter um período natural de ao menos . O seu projeto vai funcionar? Se não, explique qualitativamente o que você precisaria fazer para que ele passe a funcionar.

Vamos fazer um esquema da situação (não vamos representar a espessura para deixar o desenho mais claro, mas lembre que ela está lá):

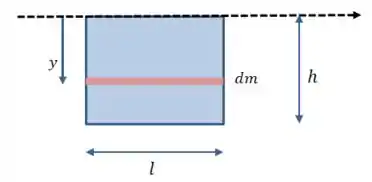
E para calcular o momento de inércia, vamos precisar de uma expressão para a densidade da porta:

E vamos montar a integral para calcular o momento de inércia. Vamos integrar “faixas” de massa que estão a uma distância do nosso eixo:

E o volume pode ser expresso como , já que estamos variando apenas a distância na direção da altura:

Agora vamos integrar isso quando varia de até :

Substituindo a nossa expressão para :

Agora vamos voltar à expressão para o período do pêndulo físico:

E substituindo os valores numéricos:

Mas o enunciado mencionou que o gato precisava de pelo menos para poder atravessar a porta. Olhando para a fórmula, a única forma de atingir isso seria aumentando a altura .