Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 14.1 - Ex. 82
Um pêndulo, em seu laboratório de física, tem um comprimento de e uma bolinha de de massa. Para iniciar o balanço da bolinha, você coloca um ventilador próximo à ela, soprando uma corrente horizontal de ar. Enquanto o ventilador está ligado, a bolinha fique em equilíbrio com o pêndulo deslocado de um ângulo de com a vertical. O vento é soprado pelo ventilador a . Você desliga o ventilador e deixa que o pêndulo oscile. (a) Supondo que a força de arraste do ar seja da forma , determine a constante de tempo de decaimento deste pêndulo. (b) Quanto tempo levará para a amplitude do pêndulo chegar a ?
Passo 1
Precisamos encontrar uma expressão para a constante de tempo nesse caso especial. Vamos analisar o torque resultante agindo sobre o pêndulo:
Onde é a aceleração angular do pêndulo.
O torque gerado pela força peso, quando o pêndulo está deslocado por um ângulo em relação à horizontal é:
Já que a força de arraste aponta sempre na horizontal, e estamos considerando pequenas oscilações, o torque da força de arrasto é:
E favorece o aumento do ângulo , e favorece o retorno ao equilíbrio, por isso os sinais.
Então:
E o momento de inércia do pêndulo simples é:
Passo 2
Mas pelo enunciado, a força de arrasto é:
Então a nossa equação é:
E para pequenos ângulos, podemos usar a seguinte aproximação:
E essa é uma equação diferencial homogênea de segunda ordem, e nós já conhecemos a forma geral da sua solução:
Onde:
Passo 3
(a) Agora vamos fazer um esquema da situação:
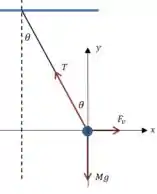
Sendo que o pêndulo está em equilíbrio quando o deslocamento angular é máximo, então:
Ficamos com o seguinte sistema:
Dividindo a primeira equação pela segunda:
E agora podemos substituir essa expressão para na fórmula que encontramos para :
Passo 4
(a) Vamos olhar de novo para a nossa equação para :
E a amplitude é todo o fator que está multiplicando o cosseno, então:
Onde , e , queremos enconrar o valor de para o qual :
Tirando o logaritmo dos dois lados:
Resposta
(a) .
(b) .