Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 11.Problemas - Ex. 12
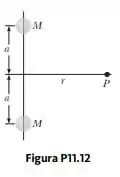
(a) Calcule o vetor campo gravitacional em um ponto sobre a mediatriz da linha que une os dois corpos de massa igual, separados por uma distância de , como mostrado na Figura P11.12. (b) Explique fisicamente por que o campo deve tender a zero quando. (c) Prove matematicamente que a resposta ao item (a) se comporta dessa maneira. (d) Explique fisicamente por que o módulo do campo deve se aproximar de quando (e) Prove matematicamente que a resposta ao item (a) se comporta corretamente nesse limite.
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Letra a:
Passo 2
Letra b:
Em r = 0, os campos dos dois objetos são iguais em magnitude e opostas na direção, para somar a zero.
Passo 3
Letra c:
Como
Passo 4
Letra d:
Quando r é muito maior do que a, os ângulos que os vetores do campo fazem com o eixo x tornam-se menores. Em distâncias muito grandes, os vetores são quase paralelos ao eixo; portanto, eles começam a se parecer com o vetor de campo de um único objeto de massa 2M.
Passo 5
Letra e:
À medida que r torna-se muito maior do que a, a expressão se aproxima de:
Resposta
- Em r = 0, os campos dos dois objetos são iguais em magnitude e opostas na direção, para somar a zero.
- Quando r é muito maior do que a, os ângulos que os vetores do campo fazem com o eixo x tornam-se menores. Em distâncias muito grandes, os vetores são quase paralelos ao eixo; portanto, eles começam a se parecer com o vetor de campo de um único objeto de massa 2M.