Velocidade e Aceleração do MHS

Teoria

A gente já viu como funciona a posição no MHS e como interpretar o gráfico, mas já te aviso que não é só isso que importa, temos outras duas grandezas que vamos precisar saber calcular e também analisar o gráfico que são a aceleração e a velocidade. Vamos aprender isso na prática, se liga nesse sistema massa-mola.

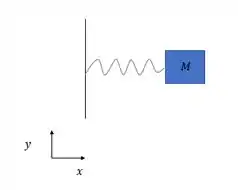
E tem a seguinte equação da posição e o seguinte gráfico de posição:

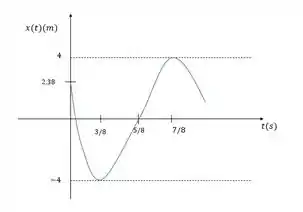
Para esse sistema, determinar as funções da velocidade e aceleração, assim como suas componentes máximas, e esboçar cada gráfico em função do tempo.

Funções aceleração e velocidade

Bom, vamos lembrar que a velocidade é a derivada da posição. Então, a gente tem.

E, pela regra da cadeia, a gente vai de dentro pra fora e aqui estamos derivando para

E, multiplicando os termos, a gente tem:

Como no outro movimento tínhamos a amplitude, só o que mudou agora é que teremos a velocidade máxima multiplicando o seno:

E a aceleração? Lembra dela? É a derivada da velocidade!

De novo, vamos à regra da cadeia derivando de dentro pra fora e multiplicando os dois.

E aí:

E aqui, multiplicando o cosseno, temos o que chamamos de aceleração máxima:

A gente viu aqui que a posição, velocidade e aceleração estão relacionadas, também podemos colocar essas relações em função das constantes, lembra que a função da posição tinha essa galera aqui?

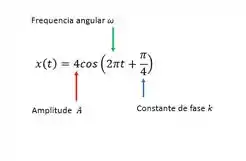
Se a gente quiser uma equação geral onde temos que substituir os valores conhecidos, podemos escrever o seguinte:

Daí a equação da velocidade fica:

E, então, pela regra da cadeia:

Esse carinha que aparece multiplicando o seno tem nome: é a velocidade máxima:

E, pra aceleração, teremos:

E, pela regra da cadeia:

E esse carinha aí que aparece multiplicando o seno também tem nome e é chamado de aceleração máxima, como a gente falou lá em cima:

Saber a relação pode ser útil na hora de analisar os gráficos ou até mesmo de calcular numa próxima, lembrando que na maioria das vezes a função da posição vem como cosseno, mas as vezes pode aparecer como seno, mas a forma de derivar é a mesma. Outro ponto interessante é que a frequência angular e a constante de fase não mudam, são as mesmas pras 3 funções.

Gráficos

Bom, a gente pode montar os gráficos de aceleração e velocidade de algumas formas diferentes. Como as funções seno e cosseno são limitadas por [-1,1], a gente pode encontrar os valores de para os quais o seno ou o cosseno são máximos, mínimos ou zero e também o tempo pra posição

Mas o jeito mais fácil quando a gente já tem o gráfico da posição é entender a relação entre eles. Um é gráfico de cosseno e o outro é gráfico de seno, a diferença deles é que o cosseno é adiantado em relação ao seno de ou seja a função chega no valor antes da outra, se liga:

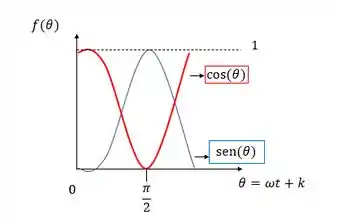
Do gráfico podemos dizer, então, que:

Ou:

Só temos que ficar ligados que no nosso caso o eixo que trabalhamos é o tempo e não o ângulo sendo assim, se a gente rearrumar pro tempo que tá no gráfico, podemos ver o seguinte pra função cosseno a gente tem:

E, rearrumando para o tempo, temos:

E, para o seno que é deslocado, temos:

E, por fim:

Assim, podemos dizer o seguinte:

E, no caso do nosso gráfico, a gente sabe que:

Então:

Por fim, vamos esboçar o gráfico comparando com o outro. Podemos fazer sem o sinal e depois inverter só pra gente ver como fica a defasagem.

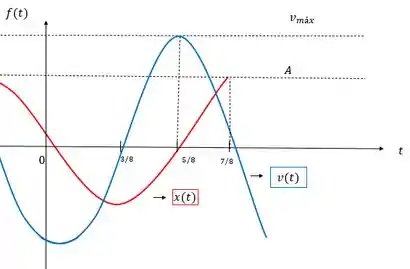
Repare que a defasagem foi exatamente de e também o gráfico ficou maior porquê a velocidade máxima é maior que a amplitude, só faltou a gente inverter o sinal do gráfico e teremos o gráfico da velocidade.

Gráfico comparado com o gráfico .

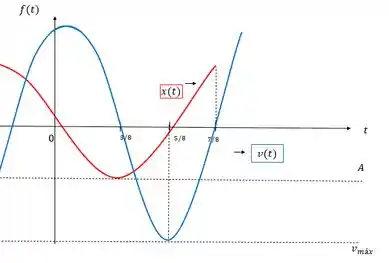
No nosso caso a amplitude é 4, e a velocidade

Pra aceleração a parada é mais tranquila, a função é cosseno também então não tem defasagem, porém a amplitude muda e o sinal também daí teremos um gráfico maior e invertido, se liga!

Gráfico comparado com o gráfico .

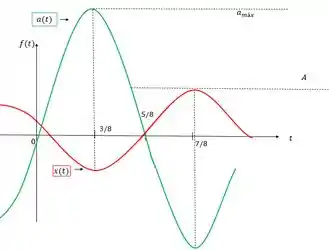
Onde nossa aceleração máxima é:

E aí está, esboçamos os gráficos comparando com o gráfico da posição. No seu caso você não precisa desenhar o gráfico da posição junto com os outros, aqui a gente fez assim pra mostrar a relação entre eles, ok?

Gráficos

Exercícios Resolvidos

Exercício Resolvido #1

Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 110-66

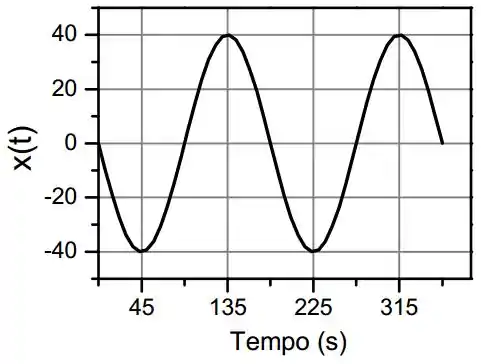
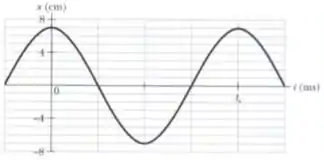
A figura abaixo mostra a posição de um bloco oscilando em MHS na extremidade de uma mola . Quais são

a) a velocidade e b) o módulo da aceleração radial de uma partícula circular uniforme correspondente?

Passo 1

Bom, a gente quer achar a velocidade do MCU correspondente a esse MHS.

Lembre-se que a velocidade do MCU pode ser escrita como:

Onde, no caso, , ou seja, o raio do MCU é igual a amplitude do MHS.

Olhando no gráfico, percebemos que

Então:

Mas não sabemos o valor de . Porém, fica fácil descobrir pelo gráfico o valor do período. Olhando direito, percebemos que ;

Assim:

Passo 2

A aceleração radial da qual o enunciado fala é a aceleração centrípeta.

Essa é dada por:

Agora é só fazer e substituir os valores:

Resposta

Exercício Resolvido #2

Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 112-100-Modificada

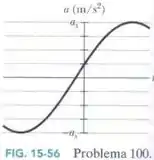
Qual é a constante da fase do oscilador harmônico cuja função aceleração aparece na Fig. 15-56 se a função posição é da forma e ?

Passo 1

Aqui a gente vai seguir o nosso esquema pra determinar a fase do oscilador. Porém, temos uma diferença: o nosso gráfico é da aceleração, já a função dada, do deslocamento.

Assim, precisamos lembrar que se:

Perceba que a gente apenas derivou ali em cima.

Passo 2

Agora vamos olhar no gráfico: o é a quarta divisão na escala vertical. Logo, como , cada divisão valerá

Pelo gráfico, a gente consegue perceber que o valor da aceleração quando vale .

Passo 3

Assim, podemos dizer que:

Repare que aqui o é a amplitude da aceleração, que vale:

Como o gráfico que temos é da aceleração, podemos usar o direto como a amplitude dele, porque já temos essa amplitude, sem precisar fazer . Beleza? Então:

Assim, considerando o intervalo de :

Também poderíamos ter: . E agora, como saber qual é o valor correto?

Passo 4

Bom, podemos pensar que a derivada da curva é dada por:

Em , essa derivada é igual a inclinação da reta tangente na curva nesse ponto. Podemos observar que essa inclinação é positiva, logo:

Como , temos que ter:

Logo, só o ângulo de satisfaz essa inequação.

Resposta

Exercício Resolvido #3

PUCRIO-P1-2013.1-Q2

Durante um conserto de uma roda-gigante com raio de metros, um técnico deixa apenas um dos carrinhos instalado. Para testes, a roda é acionada por volta de meio-dia, até atingir uma velocidade angular constante correspondente a uma volta a cada segundos, no sentido anti-horário. O técnico então observou que a sombra do carrinho projetada no chão descreve um movimento harmônico simples. Suponha que o técnico começou a observar a sombra quando o carrinho se encontrava no alto da trajetória. (Adote o ponto central da projeção como origem do eixo e considere que a sombra possui velocidade inicial negativa).

Encontre a amplitude do movimento da sombra projetada no solo.
Encontre o período e a frequência angular deste movimento.
Escreva as equações que descrevem a posição, a velocidade e a aceleração da sombra em função do tempo neste movimento harmônico simples.
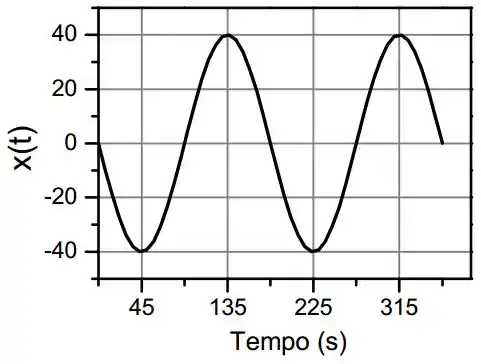
Faça um gráfico da sombra em função do tempo para dois períodos. No gráfico devem estar indicados, numericamente, os valores máximo e mínimo da posição e os tempos em que a sombra atinge esses pontos.

Passo 1

Galera, aqui a gente precisa perceber apenas uma coisa: um MHS pode ser encarado como uma projeção de um MCU.

A figura abaixo ilustra isso:

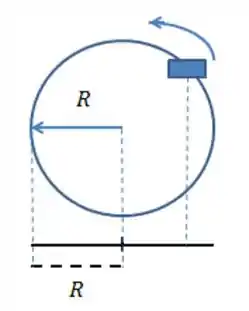
Tá vendo a linha preta embaixo do círculo? Essa é a representação do MHS.

Bom, com isso, podemos responder a primeira pergunta: qual a amplitude?

Pela figura, percebemos que a amplitude é o raio do círculo.

Então:

Passo 2

Seguindo a mesma idéia de antes, é fácil perceber que o período, frequência e a frequência angular do movimento serão os mesmo que o do MCU.

Então, o período do MHS já está dado no enunciado.

Segundo o enunciado, a roda gigante completa uma volta a cada . Isso quer dizer que o período é justamente esse:

E a frequência angular é:

Passo 3

A posição segue o modelo dos MHS e é dada por:

Já sabemos quase tudo, menos a fase ().

Bom, a informação que temos é que o movimento do carrinho, e de sua sombra, começa quando o carrinho se encontra no ponto mais alto da trajetória. Nesse caso, a projeção da sua sombra se encontra na origem do sistema que descreve o MHS( aquela linha preta lá de cima).

Então, depois de tanto blá blá blá, o que quero dizer é que: