Reflexão e Inversão de Pulsos em Corda
Produzido por Leonardo de BemTeoria
Reflexão e Inversão de Pulsos em Corda
E agora, vamos dar uma olhada em como as ondas se comportam.
A primeira coisa que vamos ver aqui é como as ondas são refletidas quando chegam a uma extremidade do meio.
É comum também considerarmos apenas um pulso, ou seja, uma única perturbação que se desloca, de tal forma:
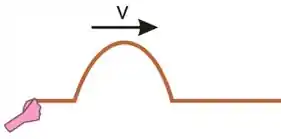
Então vamos ver os tipos de extremidade, que são dois: extremidade fixa e extremidade livre.
- Extremidade fixa:
- Extremidade livre:
O pulso é refletido com amplitude invertida. Dizemos, neste caso, que o pulso inverteu de fase:
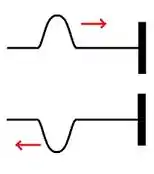
Ou seja: o pulso volta de cabeça pra baixo.
Só muda a direção da velocidade do pulso. Dizemos, neste caso, que o pulso manteve a mesma fase:
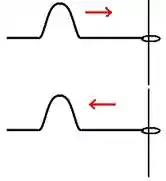
Nesse caso, o pulso volta do mesmo jeito que foi.
Usando a equação de onda em problemas de reflexão
Em alguns casos, a gente vai precisar usar o conceito de equação de onda se relacionando com reflexão.
Lembra da equação diferencial da onda?
Então, vimos que ela tem uma solução geral, que é assim:
Onde e são funções quaisquer. Beleza? Bom, mas pra que usamos isso?
Vamos fazer um exemplo:
A onda de equação está se propagando em uma corda homogênea. Em , essa corda tem uma extremidade fixa. Escreva a equação da onda refletida.
Solução:
Em , existe um nó, já que ali que os pulsos da onda se invertem. Assim, podemos dizer que:
Além disso, como o enunciado te deu , você precisa encontrar a , que retrata a onda refletida, que vai se somar com a onda que tá vindo, retratada por .
Antes da reflexão, não existia essa parcela de equação que retrata a onda refletida.
Era como se:
Então:
Beleza? Mas como o produto de uma velocidade pelo tempo nos dá uma distância, podemos fazer a seguinte mudança:
Então:
Agora, fazendo mais uma mudança de variável:
Então:
E pronto! A solução é:
Pulso passando de uma corda pra outra
Agora vamos ver um ultimo caso, que é quando um pulso passa de uma corda para outra de material diferente.
Vamos imaginar primeiro a seguinte situação: um pulso passando para uma corda com densidade linear de massa maior que a anterior.
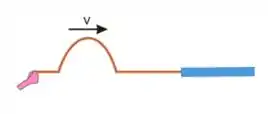
E agora o que vai acontecer?? Então, nesse caso, o pulso inverterá a sua fase (como se tivesse uma extremidade fixa!)

Beleza! Mas e se o contrario acontece? E se o pulso passa para uma corda com densidade linear de massa menor que a anterior?
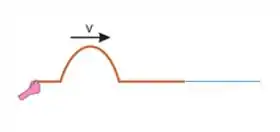
Bom, nesse caso não tem inversão de fase!
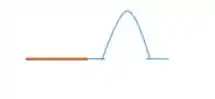
Era isso que eu tinha pra falar pra você! Bora pros exercícios agora?
Usando a equação de onda em problemas de reflexão
Pulso passando de uma corda pra outra
Agora vamos ver um ultimo caso, que é quando um pulso passa de uma corda para outra de material diferente.
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Física 2, Prova 2, 2014.1 – Questão M01
Dois pulsos de formas diferentes se propagam com velocidade numa corda esticada de comprimento . A corda tem sua extremidade esquerda fixa num suporte, mas a extremidade da direita pode oscilar livremente. Num dado instante a situação da corda é aquela mostrada na figura. Esta EXATA situação irá se repetir exatamente após um intervalo de tempo mínimo dado por:
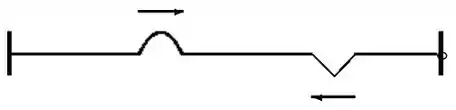
Passo 1
Vamos ver como fica cada momento refletindo nos dois pontos, o da direita não muda a fase, enquanto o da esquerda inverte.
No início temos a figura da questão, depois fica
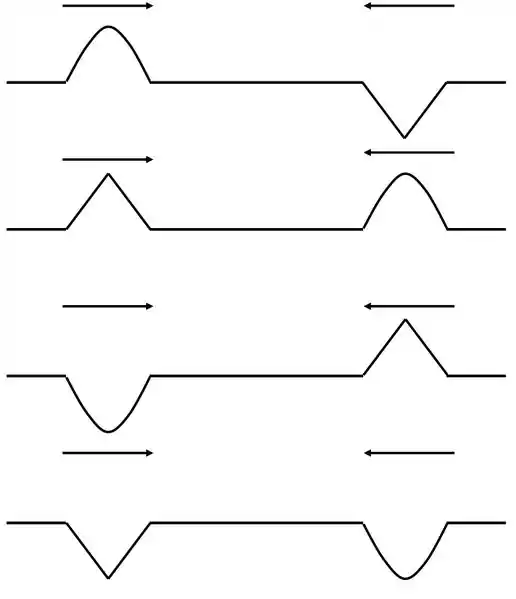
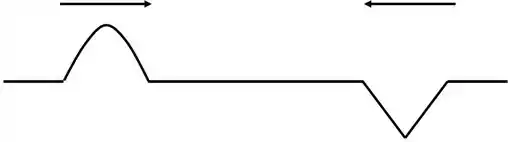
Da primeira para a segunda ele anda , da segunda para a terceira de novo , e assim por diante, até ir da quarta para a quinta, que é a posição inicial.
Isso resulta em:
Vamos ter:
Resposta
Letra D
Exercício Resolvido #2
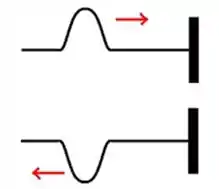
Uma onda é enviada por uma corda homogênea presa pela extremidade da direita. O perfil instantâneo da onda está ilustrado na figura abaixo.
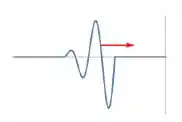
Identifique o perfil instantâneo da mesma onda depois que ela se reflete na extremidade direita da corda.
a)
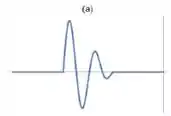
b)
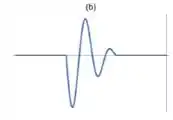
c)
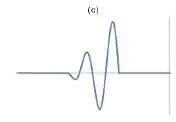
d)
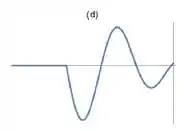
e)
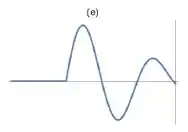
Passo 1
Como a extremidade é fixa, o pulso é refletido com amplitude invertida. Além disso, o ponto que chegou primeiro à extremidade direita, presa, é o primeiro ponto a voltar. Consequentemente o último a chegar é o último a voltar.
A resposta que é mais se adéqua a essas duas coisas é a da A.
Resposta
Letra A.
Exercício Resolvido #3
A figura mostra duas fotografias de um pulso numa corda feita de dois materiais diferentes, unidos por uma junção indicada pela linha pontilhada. A fotografia superior foi tirada antes do pulso gerado à esquerda atingir a junção e a fotografia inferior, num instante posterior à chegada do pulso à junção.
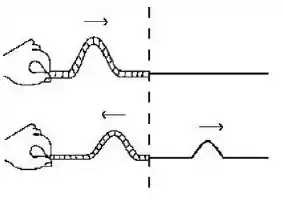
Pode-se concluir que:
a) O comprimento de onda do pulso transmitido é menor que aquele da onda refletida.
b) O material à direita da junção é mais denso que o à esquerda.
c) A junção atua como uma extremidade fixa.
d) O material à esquerda da junção é mais denso que o à direita.
e) A situação é fisicamente impossível, já que os pulsos incidente e refletidos devem ter a mesma altura.
Passo 1
Se o pulso refletido tem a orientação oposta ao pulso incidente então a corda de onde veio o pulso tem densidade linear de massa menor.
Se o pulso refletido tem a mesma orientação que o pulso incidente então a corda de onde veio o pulso tem densidade linear de massa maior.
Assim como o pulso refletido tem a mesma orientação que o pulso incidente a corda à esquerda tem densidade de massa maior.
Resposta
Letra (D)
Exercício Resolvido #4
UFRJ, Física 2, Prova 2, 2015.1 – Questão 3
Considere uma onda dada por que atinge a extremidade de uma corda, fixa em Neste caso, qual é a forma da onda refletida?
Passo 1
Bom, galera, aqui a gente vai ter que usar o conceito de solução geral da equação de onda unidimensional:
A solução geral é:
O que vamos fazer aqui? Bem, o enunciado nos deu uma função parecida com a primeira equação acima. A nossa missão é achar a outra:
No entanto, vamos prestar atenção numa coisa. Antes que a onda bata lá em , nós consideramos que:
Vamos lá.
Passo 2
Bom, a onda inverte a sua fase em .:
Então, ali .
Show? Então vamos escrever:
Passo 3
Beleza?
Bom, mas o produto de uma velocidade com tempo nos dá uma distância, certo? Então podemos fazer isso:
Então:
Ok. Mas as equações acima são funções. Então podemos usar mudança de variáveis ali.
Como queremos encontrar o valor de:
Podemos chamar:
Assim:
Pronto (:
d)
Resposta
d)
Exercício Resolvido #5
Um pulso que se propaga com velocidade de v = 30 m/s numa corda de comprimento com a extremidade x = L fixa é descrito pela função , onde = 15 cm e a = 8,0 . A função que representa o pulso refletido em um instante t logo após sua primeira reflexão em x = L é:
a)
b)
c)
d)
e)
Passo 1
Antes de sair explicando, um parênteses....(expressão um pouco assustadora essa , né?)
Bom, mas não se assuste, jovem...Vamos ver que a questão é bem tranquilinha ![]()
Vamos chamar a nossa onda assustadora de uma . Por que isso? Só porque identificamos esse termo na expressão, beleza?
Show de bola...Sendo assim, a onda refletia será uma função , certo? Uma função de onda qualquer, mas com sinal positivo no porque ela ta se propagando no sentido contrário da onda original.
A onda que tá se propagando na corda é do tipo:
Veja que antes da reflexão do pulso:
Então:
Beleza! Como a extremidade L é fixa, vamos ter, depois da reflexão:
E eu quero achar , a onda refletida!
Show! Agora eu vou usar uma variável auxiliar aqui:
Com essa variável eu posso escrever:
Porque, quando :

Então:
E como:
Então a equação do pulso refletido vai ser:
Resposta
Letra E.