Pulso Não-Harmônico
Teoria
Vimos até aqui ondas se propagando na corda de maneira harmônica, seguindo a equação geral com as funções seno e cosseno. Mas será que existe algo diferente disso?
Sim! O enunciado pode dar uma equação que pode representar um pulso e não uma onda.
Essa equação pode ser do tipo:
Existem algumas coisas que podem ser pedidas a partir dessa equação, são elas:
- O pulso, ou seja, , quando ;
- A velocidade de propagação do pulso;
- A velocidade transversal de um dado ponto da corda em um instante .
Cálculo do pulso
Calcular o pulso quando é simples. Basta substituir a variável por zero e obter a equação , ok?
Aí se ele pedir o gráfico de em função de , basta encontrar os valores da função quando:
E teremos os valores para esboçar o gráfico.
Cálculo da velocidade de propagação
Já para o cálculo da velocidade de propagação, temos que fazer uma mudança de referencial. Vamos para um referencial que se move com a mesma velocidade de propagação do pulso.
Com isso, a gente começa a analisar um pulso parado, né? Se liga:
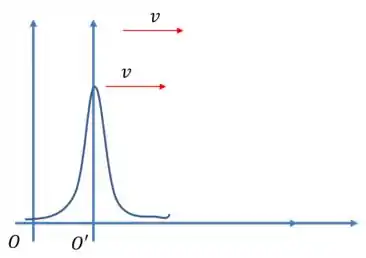
Vamos fazer um exemplo.
Se a função de um pulso variando com e é dada por:
Para mudar de referencial, temos que mudar a variável para uma nova variável , tal que a função se transforme em .
No nosso exemplo, é necessário que o termo desapareça, então:
O que resultaria em:
E essa última equação é a que descreve o pulso estacionário, no referencial .
Portanto, a equação que relaciona e nos dá a velocidade com que o referencial está se movendo. Como essa velocidade de é igual a velocidade de propagação da onda, temos:
Para descobrir o sentido da propagação, se liga no bizu:
- Se negativo;
- Se positivo.
Cálculo da velocidade transversal
Por último, temos o terceiro item, que nos pede a velocidade transversal de um ponto em um instante . Não tem mistério! Basta derivar parcialmente a equação do pulso em função de .
Vamos usar o exemplo do item anterior:
Derivando parcialmente:
Algumas contas aqui podem ficar difíceis, portanto, é essencial que você pratique. Bora lá!
Cálculo do pulso
Cálculo da velocidade de propagação
Cálculo da velocidade transversal
Exercícios Resolvidos
Exercício Resolvido #1
USP-P1-2014.1-Q11- letras a, b, c.
Um pulso, se movendo em uma corda esticada com tensão , é descrita pela função de onda:
- Faça um gráfico de como função de .
- Qual o valor da magnitude da velocidade de propagação do pulso e sua direção?
- Calcule a velocidade transversal de um dado ponto da corda num instante
Passo 1
a)
Bom, aqui nós vamos ter que primeiro fazer uma manipulação de variáveis pra encontrar a nossa função :
Isolando no denominador e no numerador:
Se a gente fizer , vamos obter o valor 1. Se a gente fizer tender ao infinito, a função tende a zero, assim como se a gente fizer tender a menos infinito.
Logo, o gráfico da função fica:
Passo 2
b)
Se a gente considerar um observador se movendo na mesma direção do pulso e com a mesma velocidade que ele, esse observador o veria parado, certo? Ou seja, sem dependência temporal.
Se a gente reescrever a função do pulso excluindo a parte que funciona como uma função do tempo (no caso , podemos escrever:
Legal...Mas e daí?
Bom, agora a gente tem que pensar em como fizemos essa transformada. Se a gente tomar:
E depois substituir na equação original:
Que é a equação do pulso parado.
Só que a equação é justamente a equação de um móvel se movendo com velocidade na direção positiva do eixo
Logo, como estávamos supondo que esse observador estava se deslocando na mesma velocidade que o pulso, a velocidade do pulso será:
Passo 3
c)
Bom, pra se calcular a velocidade transversal de um ponto na corda num instante qualquer, a gente precisa derivar parcialmente a função em relação a . Ou seja:
Isso acontece porque a gente ‘congela’ um qualquer e apenas varia o tempo dele, ou seja, o ponto passa a se mover pra cima e pra baixo, apenas transversalmente.