Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Oscilador Harmônico Quântico

Ver Todos os Exercícios

Teoria

Fala aí, seja bem vindo ao Responde Aí! Bora aprender sobre Movimento Harmônico Quântico?!

Lá na Física Clássica a gente estuda o movimento harmônico simples e é bem comum a gente ver esse tipo de sistema massa-mola, onde colocamos uma massinha na ponta de uma mola, e deixa ela oscilando:

Movimento Harmônico: Sistema Massa Mola
Movimento Harmônico: Sistema Massa Mola

Mas imagina se…ao invés de um pesinho qualquer, a gente colocasse dois átomos presos por uma mola! 😱

Oscilador Harmônico Quântico
Oscilador Harmônico Quântico

Esse é o espirito do Oscilador Harmônico Quântico! Essa “mola” é nada mais nada menos do que a ligação entre dois átomos, formando uma molécula diatômica! 🤩

Bora entender como isso funciona?!

📢 Clique para ver mais:

Como Funciona um Oscilador Harmônico Quântico?

Os cálculos iniciais do Oscilador Harmônico Quântico e o raciocínio é beem parecido com o MHS! A energia potencial de uma partícula de massa , presa a uma mola de constante elástica , é dada por:

Onde:

Colocando isso em um gráfico, ficamos com:

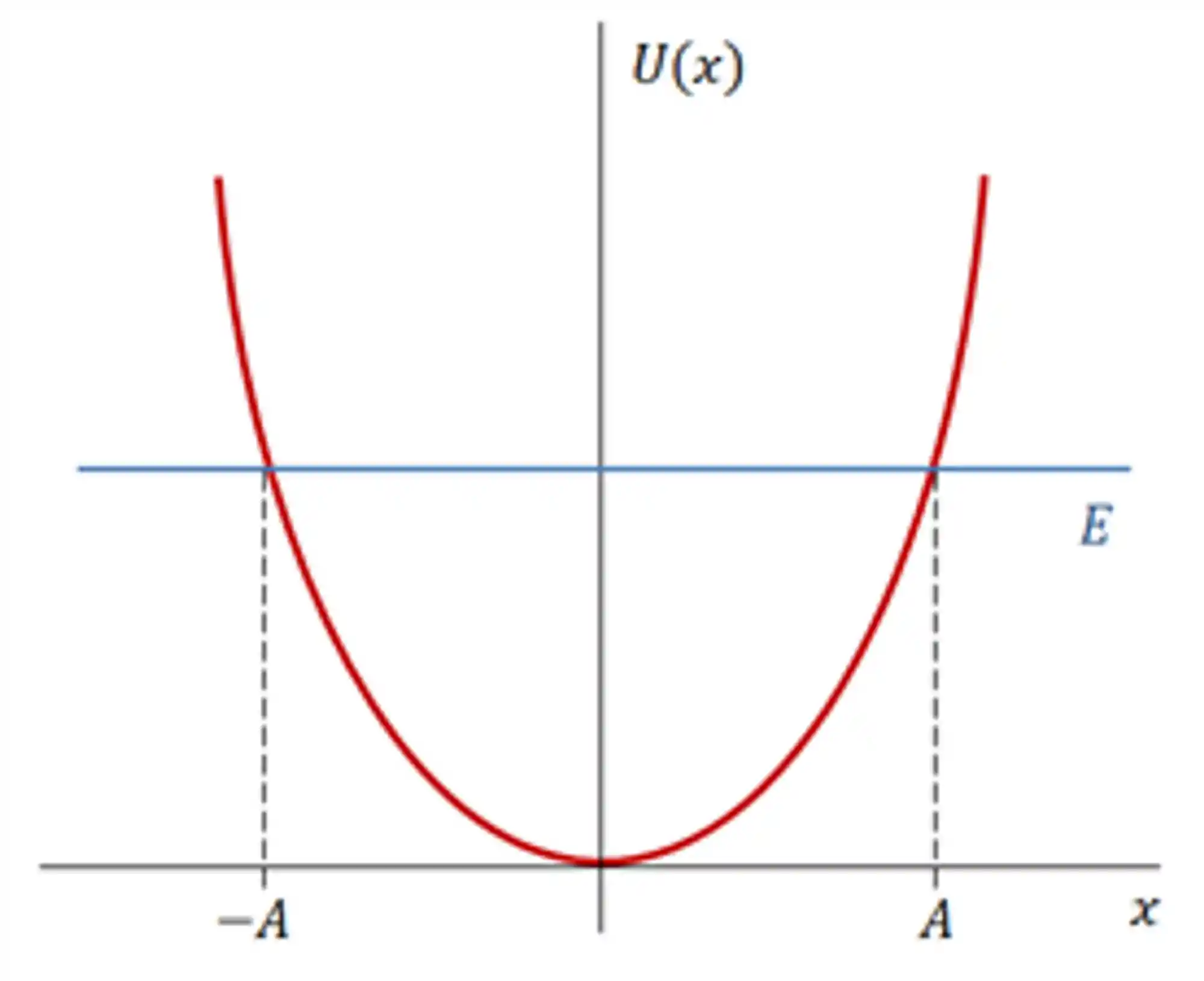
Oscilador Harmônico: Gráfico
Oscilador Harmônico: Gráfico

Substituindo a função de energia potencial na Equação de Shrödinger temos:

Nessa equação os estados vão ser quantizados, sendo o estado fundamental dado por:

E os outros estados vão ser multiplicados pelos Polinômios de Hermite. A energia do estado fundamental pode ser calculada por:

Essa energia é chamada de energia de ponto zero do oscilador harmônico. Nunca teremos a partícula com energia zero, a sua menor energia vai ser ! Podemos calcular a energia em cada estado com a seguinte fórmula:

Graficamente temos:

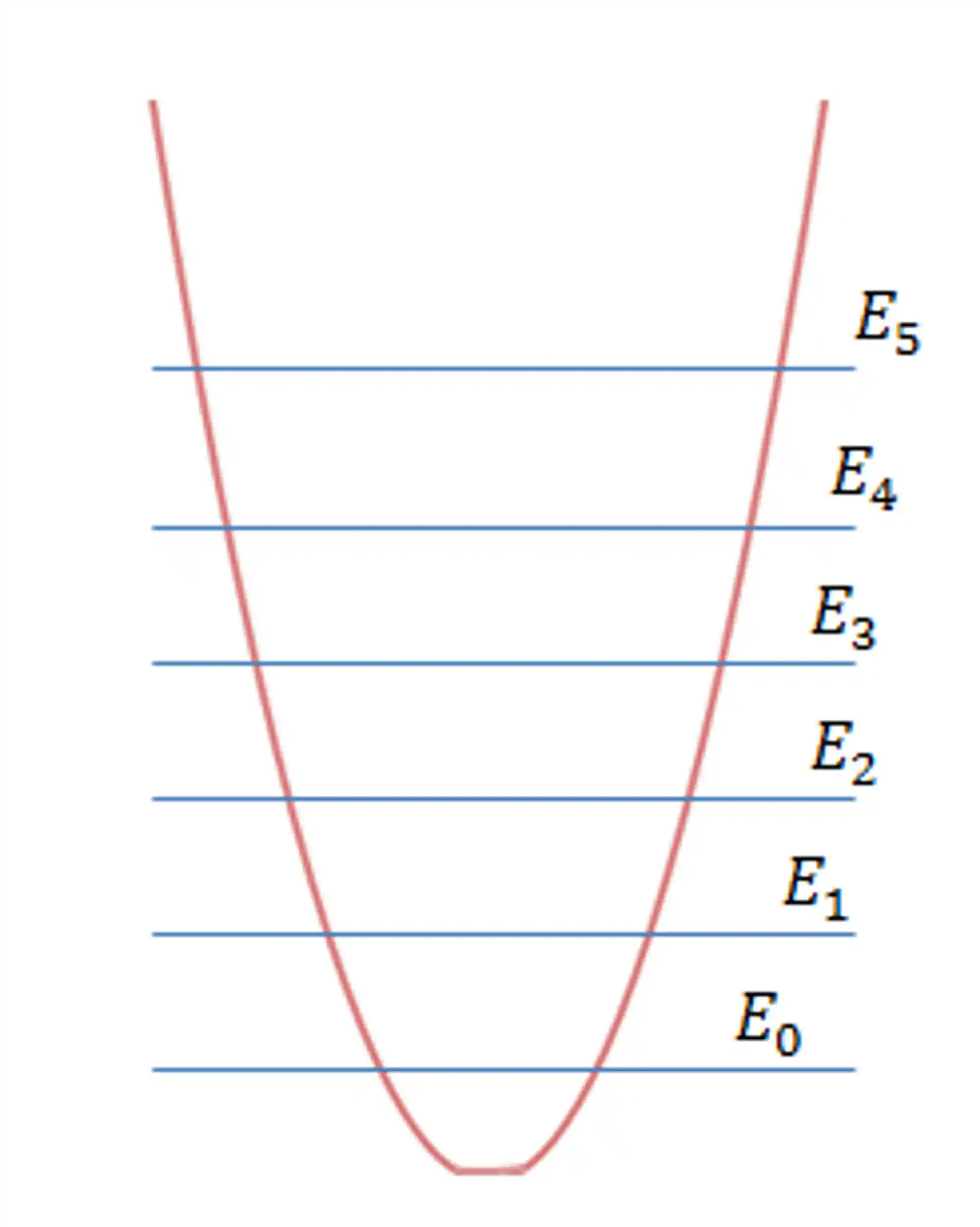
Você também pode conferir esse conteúdo em vídeo:

Agora vamos praticar com exercícios?

Exercícios Resolvidos

Exercício Resolvido #1

Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 261-40.27

Um bloco de madeira com massa igual a 0,250   k g oscila na extremidade de uma mola cuja constante é igual a 110   N / m .

Calcule a energia do nível fundamental e a diferença de energia entre dois níveis adjacentes. Expresse sua resposta em joules e em elétrons-volt.

Os efeitos quânticos são importantes?

Passo 1

A energia no estado fundamental é dada por:

E 0 = 1 2 ℏ ω 0

E 0 = ℏ 2 k m

Onde:

ℏ = 1,05 × 10 - 34   J s ;

k = 110   N / m ;

m = 0,250   k g ;

Logo:

E 0 = 1,05 × 10 - 34 2 × 110 0,25

E 0 = 1,11 × 10 - 33   J = 6,90 × 10 - 15   e V

Lembrando que 1   e V = 1,6 × 10 - 19   J .

Passo 2

A energia em qualquer nível é dada por:

E n = n + 1 2 ℏ ω 0

Assim, a energia entre dois níveis adjacentes será:

E n + 1 - E n = n + 1 + 1 2 ℏ ω 0 - n + 1 2 ℏ ω 0

E n + 1 - E n = ℏ ω 0 = ℏ k m

Passo 3

E n + 1 - E n = ℏ k m

Onde:

ℏ = 1,05 × 10 - 34   J s ;

k = 110   N / m ;

m = 0,250   k g ;

Logo:

E n + 1 - E n = 1,05 × 10 - 34 × 110 0,25 = 2,20 × 10 - 33   J = 1,38 × 10 - 14   e V

E n + 1 - E n = 2,20 × 10 - 33   J = 1,38 × 10 - 14   e V

Passo 4

Os efeitos quânticos são importantes?

Não, pois as energias são muito pequenas para massas relativamente grandes.

Resposta

1,11 × 10 - 33   J = 6,90 × 10 - 15   e V

2,21 × 10 - 33   J = 1,38 × 10 - 14   e V

Não, pois as energias são muito pequenas para massas relativamente grandes.

Exercício Resolvido #2

Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 261-40.29, modificado

Os químicos usam espectros de absorção infravermelho para identificar os elementos químicos em uma amostra.

Em certa amostra, um químico verifica que uma luz de comprimento de onda 5,8   μ m é absorvida.

  1. Calcule e a energia dessa transição.

    2. (Obs: Considere que é uma transição entre dois níveis de energia adjacentes)

  2. Se a massa da molécula é 5,60 × 10 - 26   k g , calcule a constante da mola.

Passo 1

Letra (a): Calcule e a energia dessa transição.

Podemos relacionar a energia da transição com o comprimento de onda através da relação:

E = h f = h c λ

Onde:

h = 6,626 × 10 - 34   J s ;

c = 3 × 10 8   m / s ;

λ = 5,8   μ m = 5,8 × 10 - 6   m ;

Logo:

E = 6,626 × 10 - 34 × 3 × 10 8 5,8 × 10 - 6

E = 3,43 × 10 - 20   J = 0,21   e V

Lembrando que 1   e V = 1,6 × 10 - 19   J .

Passo 2

Letra (b): Se a massa da molécula é 5,60 × 10 - 26   k g , calcule a constante da mola.

A energia em qualquer nível é dada por:

E n = n + 1 2 ℏ ω 0

Se houve uma transição de um nível para outro adjacente, essa variação de energia é dada por:

E = E n + 1 - E n = ℏ ω 0 = ℏ k m

Passo 3

E = ℏ k m

k = E 2 m ℏ 2

Onde:

ℏ = 1,05 × 10 - 34   J s ;

E = 3,43 × 10 - 20   J ;

m = 5,60 × 10 - 26   k g ;

Logo:

k = 5975   N / m

Resposta

Letra (a):

0,21   e V

Letra (b):

5975   N / m

Exercício Resolvido #3

Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 261-40.33, modificado

Para um átomo de sódio que oscila com frequência angular ω 0 = 1,79 × 10 13   r a d / s , calcule:

  1. A energia do estado fundamental;
  2. O comprimento de onda de um fóton emitido quando ocorre a transição de n = 4 para n = 3 ;
  3. A diferença de energia para qualquer transição em que Δ n = 1 ;

Passo 1

Letra (a): A energia do estado fundamental;

A energia do estado fundamental é dada por:

E 0 = 1 2 ℏ ω 0

Onde:

ℏ = 1,05 × 10 - 34   J s = 6,582 × 10 - 16   e V ;

ω 0 = 1,79 × 10 13   r a d / s ;

Logo:

E 0 = 6,582 × 10 - 16 × 1,79 × 10 13 2

E 0 = 5,9 × 10 - 3   e V

Passo 2

Letra (b): O comprimento de onda de um fóton emitido quando ocorre a transição de n = 4 para n = 3 ;

A energia no n-ésimo estado excitado é dada por:

E n = n + 1 2 ℏ ω 0

Assim, quando há a transição de n = 4 para n = 3 , a energia liberada é dada por:

Δ E = E 4 - E 3 = 4 + 1 2 - 3 - 1 2 ℏ ω 0 = ℏ ω 0

Essa energia deve ser igual à energia do fóton emitido, logo:

Δ E = ℏ ω 0 = h f = h c λ

ℏ ω 0 = h ω 0 2 π = h c λ

λ = 2 π c ω 0

Onde:

c = 3 × 10 8   m / s ;

ω 0 = 1,79 × 10 13   r a d / s ;

Logo:

λ = 2 π × 3 × 10 8 1,79 × 10 13 = 106 μ m

Passo 3

Letra (c): A diferença de energia para qualquer transição em que Δ n = 1 ;

A energia no n-ésimo estado excitado é dada por:

E n = n + 1 2 ℏ ω 0

Assim, a diferença de energia é dada por:

Δ E = E n + 1 - E n = n + 1 + 1 2 ℏ ω 0 - n + 1 2 ℏ ω 0

Δ E = ℏ ω 0

Onde:

ℏ = 1,05 × 10 - 34   J s = 6,582 × 10 - 16   e V ;

ω 0 = 1,79 × 10 13   r a d / s ;

Logo:

Δ E = 6,582 × 10 - 16 × 1,79 × 10 13

Δ E = 0,0118   e V

Resposta

Letra (a):

5,9 × 10 - 3   e V

Letra (b):

106   μ m

Letra (c):

0,0118   e V = 1,18 × 10 - 2   e V

Exercícios de Livros Relacionados

Use o procedimento do Exemplo 35-1 para verificar se a energia do primeiro estado excitado do oscilador harmônico é 2 03 E1 = = ω. (Nota: Em vez de resolver novamente, use o resultado do passo 8: 0 =
Verifique se a constante de normalização A0 na função de onda do oscilador harmônico no estado fundamental () 20 0ax x A e− = ((Equação 35-23) é dada por () 1 40 0 A = 2mω h.
Estime a força do oscilador (ver Problema 14.16) de uma transição de trans- ferência de carga que admite a migração de um elétron de um orbital 1s do hidrogênio para outro orbital 1s de outro átomo de
Mostre que as funções de estado fundamental e a primeira onda de estado excitado do oscilador harmônico são ortogonais; isto é, mostre que