Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Transformação de Lorentz para Espaço e Tempo

Ver Todos os Exercícios

Teoria

Introdução

Já percebeu o que acontece quando a gente tá dentro de um carro, ou ônibus? A nossa percepção dentro do evento é diferente de quem tá de fora. Isso acontece porquê para cada observador é definido um referencial com um sistema de coordenadas.

Vamos ver um exemplo onde dois observadores em pontos diferentes medem uma distância até um ponto x ,   se liga:

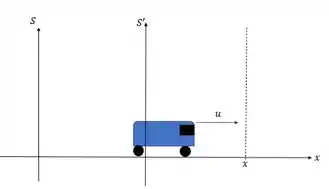
O carinha de fora que está no referencial S fixo vê a distância da posição x da seguinte forma:

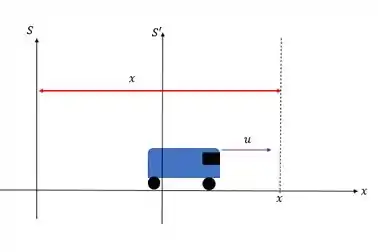
Já o outro que tá dentro do carro vê o seguinte:

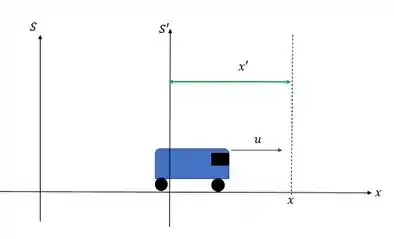
A questão é: qual a relação entre os dois sistemas de coordenadas?

Transformação de Galileu

Antes de começar a estudar relatividade, se tivéssemos que estabelecer a relação entre as coordenadas, usaríamos as Transformações de Galileu. Vamos entender essas transformações fazendo o exemplo do carro.

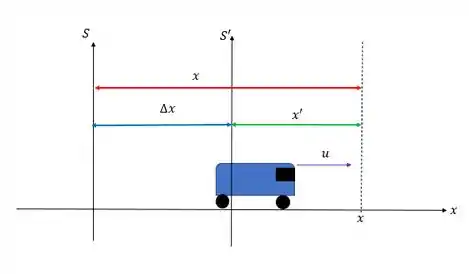
Imagina que esse carro se movimenta com u = 20 m / s , se a posição observada por S = 100 m , calcule a posição observada em S '   quando t = 3 s .

Como a velocidade que o carro se movimenta é u , a gente pode dizer que de S até S ' o espaço percorrido é:

∆ x = u t

E nesse caso pela figura a gente vê que:

∆ x = x - x '

x - x ' = u t

x ' = x - u t

E para S ' o tempo observado é o mesmo que em S :

t ' = t

Substituindo os valores pra posição x ' a gente descobre o que foi observado em S '

x ' = 100 - 20 × 3 = 40 m

Essas transformações são válidas quando a velocidade do objeto em movimento for muito menor do que a velocidade da luz.

Mas e quando as velocidades forem muito altas?

Transformação de Lorentz para as coordenadas

Lorentz reescreveu as transformações de Galileu e enfim definiu uma nova transformação que relaciona x ' com x   que funciona para todos os casos incluindo para velocidades próximas a da luz.

Vamos de novo ao exemplo do carro, porém agora ele se movimenta com velocidade u = 0,6 c . Como encontrar a posição pra S ' para o mesmo espaço x = 100 m porém agora no tempo t = 0,3 μ s .

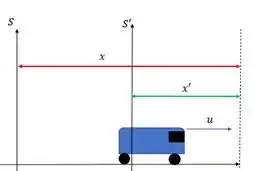
O referencial S ' se move em relação ao referencial S com velocidade u no sentido + x . Assim, as coordenadas y e z permanecem as mesmas nos dois referenciais.

Usando a transformada de Galileu e o conceito de contração do espaço vamos chegar onde queremos:

Lembrando que a contração espacial é dada por:

l = l 0 γ

A única distância que vai sofrer contração espacial é a distância não própria, que para S é a parcela de S ' , ou seja, x ' .

x ' γ = x - u t

E rearrumando, temos a relação entre as coordenadas no caso relativístico, para S ' .

x ' = γ x - u t

E pra ganharmos tempo vamos encontrar a posição pra S usando o seguinte bizu:

Vamos pegar a equação pra S '

x ' = γ x - u t

E fazer as modificações:

x → x '

t → t '

x - u t → x ' + u t '

E a equação pra posição do referencial S ficará:

x = γ x ' + u t '

Lembrando que o fator de Lorentz é:

γ = 1 1 - u 2 c 2

E pra responder a posição observada em x ' o primeiro passo é calcular o fator de Lorentz que com os valores da equação fica:

γ = 1 1 - 0,6 c 2 c 2 = 1 1 - 0,36

γ = 1 0,64 = 10 8

O fator é responsável pela distorção, e nesse caso é a contração do espaço, agora substituímos os valores pra x ' na equação da posição do referencial S ' .

x ' = γ x - u t

Lembrando que c = 3 × 10 8 m / s e 0,3 μ s = 3 × 10 - 7 s

x ' = 10 8 100 - 0,8 × 3 × 10 8 × 3 × 10 - 7

x ' = 10 8 × 28 = 35 m

Sa gente não considerasse o fator de Lorentz o resultado encontrado teria sido menor. Isso mostra que a transformação de Galileu não seria eficiente pra determinar o comprimento medido pra S ' quando a velocidade do objeto for próxima a velocidade da luz.

Também é possível relacionar o tempo que cada observador vê, que por causa da dilatação do tempo acaba sendo diferente entre S e S '

Para achar a relação entre t e t ' , bastaria isolar x ' ou x das duas equações igualá-las, assim:

x ' = γ x - u t = ⏟ D a   p r i m e i r a e q u a ç ã o - u t ' + x / γ     ⏟ D a   s e g u n d a e q u a ç ã o

O resultado para S ' é:

t ' = γ t - u x c 2

E no nosso exemplo, o tempo observado pra S ' seria:

t ' = 10 8 × 3 × 10 - 7 - 0,8 c × 100 c 2

Cortando o semelhante e substituindo o valor da velocidade da luz temos:

t ' = 10 8 × 3 × 10 - 7 - 60 3 × 10 8

t ' = 10 8 10 - 7 = 1,25 × 10 - 7 s

E como 10 - 6 s = μ s

t ' = 0,125 μ s

E repara que encontramos um tempo t ' < t , isso significa que pro observador em S o tempo sofreu dilatação.

Aplicando aquele bizu que foi usado pra posição, a gente pode encontrar a equação pro tempo em S , caso o enunciado nos dê o tempo em S ' .

Então vamos pegar a equação:

t ' = γ t - u x c 2

e trocar:

t → t '

x → x '

t - u x c 2 → t ' + u x ' c 2

E a equação do tempo para S passará a ser:

t = γ t ' + u x ' / c 2

Resumo

Bom, pra simplificar a nossa vida, se liga no resumão abaixo.

  • Transformação de S (em repouso) para S ' (em movimento):

    • x ' = γ x - u t

    y ' = y

    z ' = z

    t ' = γ t - u x / c 2

    T r a n s f o r m a ç õ e s   d e   L o r e n t z   p a r a   a s   c o o r d e n a d a s

  • Transformação de S ' (em movimento) para S (em repouso):

x = γ x ' + u t '

y = y '

z = z '

t = γ t ' + u x ' / c 2

T r a n s f o r m a ç õ e s   d e   L o r e n t z   p a r a   a s   c o o r d e n a d a s

Ah, é! Sobre as transformações de Galileu, olha só: nas situações em que u ≪ c , γ → 1 , as Transformações de Lorentz se tornam as transformações de Galileu.

Transformação de Lorentz para as coordenadas

Resumo

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ-P2-2012.1-ME01

Num referencial parado na Terra, dois estudantes de Física IV, que têm coordenadas espaciais dadas por x 1 = 300 m , x 2 = 600 m , y 1 = y 2 = 0 , z 1 = z 2 = 0 , emitem dois sinais luminosos separados por um intervalo de tempo igual a t = 10 - 6 s .

Outro estudante está numa nave que se desloca em relação à Terra com velocidade igual a v → = 0,6 c   x ^ .

As origens dos dois sistemas coincidem para t = t ' = 0 .

Qual a distância e o intervalo de tempo medidos por este estudante que está na nave, entre os dois sinais emitidos?

  1. 10 8 × 10 - 6 s ;   375 m
  2. 0,5 × 10 - 6 s ;   240 m
  3. 0,5 × 10 - 6 s ;   150 m
  4. 8 10 × 10 - 6 s ;   240 m
  5. 8 10 × 10 - 6 s ;   375 m
  6. Nenhuma das anteriores

Passo 1

De acordo com as transformações de Lorentz para o espaço de um referencial em repouso para um referencial em movimento:

x ' = γ ( x - u t )

A variação de espaço Δ x ' é dada por:

Δ x ' = γ ( Δ x - u Δ t )

Passo 2

Vamos começar calculando γ .

γ = 1 1 - u 2 c 2

Onde u = 0,6 c . Logo:

γ = 1 1 - 0,6 c c 2 = 1 1 - 0,36 = 1 0,64 = 1 0,8

γ = 10 8 = 1,25

Passo 3

Δ x ' = γ ( Δ x - u Δ t )

Onde:

γ = 1,25 ;

Δ x = 300   m ;

Δ t = 10 - 6   s ;

u = 0,6 c ;

c = 3 × 10 8   m / s ;

Logo:

Δ x ' = 1,25 × 300 - 0,6 × 3 × 10 8 × 10 - 6

Δ x ' = 150   m

Passo 4

De acordo com as transformações de Lorentz para o tempo de um referencial em repouso para um referencial em movimento:

t ' = γ t - u x c 2

Logo, o intervalo de tempo é dado por:

Δ t ' = γ Δ t - u Δ x c 2

Onde:

γ = 1,25 ;

Δ t = 10 - 6 ;

u = 0,6 c ;

c = 3 × 10 8   m / s ;

Δ x = 300   m ;

Logo:

Δ t ' = 1,25 10 - 6 - 0,6 × 3 × 10 8 × 300 ( 3 × 10 8 ) 2

Δ t ' = 0,5 × 10 - 6   s

Resposta

Letra (c): 0,5 × 10 - 6 s ;   150 m

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 181-64.

A figura abaixo mostra uma nave (cujo referencial é S ' ) passando por um observador (cujo referencial é S ) com velocidade v → = 0,95 c   i → .

Um próton é emitido com uma velocidade de 0,98 c ao longo da maior dimensão da nave, a proa para a popa. O comprimento próprio da nave é 760 m .

Determine a distância temporal entre o momento em que o próton foi emitido e o momento em que chegou à popa da nave a de acordo com um passageiro da nave e b de acordo com um observador estacionário no referencial S .

Suponha que o percurso do próton, em vez de ser da proa para a popa, seja da popa para a proa. Nesse caso, qual é a distância temporal entre o momento em que o próton foi emitido e o momento em que chegou à popa da nave c de acordo com um passageiro da nave e d de acordo com um observador estacionário no referencial S ?

Passo 1

a Determine a distância temporal entre o momento em que o próton foi emitido e o momento em que chegou à popa da nave de acordo com um passageiro da nave.

De acordo com o referencial do passageiro, o intervalo de tempo medido (no referencial S ' ) será:

Δ t ' = Δ x ' 0,98 c = 760 0,98 × 3 × 10 8

Δ t ' = 2,59 × 10 - 6   s

Δ t ' = 2,59   μ s

Passo 2

b Determine a distância temporal entre o momento em que o próton foi emitido e o momento em que chegou à popa da nave de acordo com um observador estacionário no referencial S .

Usando a transformação de Lorentz para o tempo, do referencial S ' (em movimento) para S (em repouso), teremos:

Δ t = γ Δ t ' + v Δ x ' c 2

Vamos começar calculando o fator de Lorentz, dado por:

γ = 1 1 - v c 2

Obs.: É importante ressaltar que a velocidade v é a velocidade relativa entre os dois referenciais. Logo, é ela que devemos usar para calcular o fator de Lorentz.

γ = 1 1 - 0,95 c c 2

γ = 3,2

Passo 3

Agora podemos calcular o intervalo de tempo medido no referencial S .

Obs.: Como o próton se move da direita para a esquerda, aqui devemos considerar Δ x ' negativo, logo Δ x ' = - 760 m .

Δ t = 3,2 2,59 × 10 - 6 + 0,95 c × - 760 c 2

Δ t = 5,87 × 10 - 7 s

Δ t = 0,587   μ s

Passo 4

c Qual é a distância temporal entre o momento em que o próton foi emitido e o momento em que chegou à popa da nave de acordo com um passageiro da nave?

De acordo com o referencial do passageiro, o intervalo de tempo medido (no referencial S ' ) será:

Δ t ' = Δ x ' 0,98 c = 760 0,98 × 3 × 10 8

Δ t ' = 2,59 × 10 - 6   s

Δ t ' = 2,59   μ s

Passo 5

d Qual é a distância temporal entre o momento em que o próton foi emitido e o momento em que chegou à popa da nave de acordo com um observador estacionário no referencial S ?

Usando a transformação de Lorentz para o tempo, do referencial S ' (em movimento) para S (em repouso), teremos:

Δ t = γ Δ t ' + v Δ x ' c 2

Obs.: Como o próton agora se move da esquerda para a direita, aqui devemos considerar Δ x ' positivo, logo Δ x ' = + 760 m .

Δ t = 3,2 2,59 × 10 - 6 + 0,95 c × 760 c 2

Δ t = 1,60 × 10 - 5 s

Δ t = 16 , 0   μ s

Resposta

a

Δ t ' = 2,59   μ s

b

Δ t = 0,587   μ s

c

Δ t ' = 2,59   μ s

d

Δ t = 16,0   μ s

Exercício Resolvido #3

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 178-22.

Como na figura abaixo, o referencial S ' passa pelo referencial S com uma certa velocidade.

A figura abaixo mostra a distância temporal entre dois eventos no referencial S , Δ t , em função da distância espacial entre os mesmos eventos no referencial S ' , Δ x ' , para 0 ≤ Δ x ' ≤ 400 m . A escala do eixo vertical é definida por Δ t a = 6,00   μ s .

Qual é o valor da distância temporal entre os dois eventos no referencial S ' , Δ t ' ?

Passo 1

Usando a transformação de Lorentz para o tempo, temos:

Δ t = γ Δ t ' + u Δ x ' c 2

Aqui é necessária uma certa malandragem... nós podemos usar pegar essa equação, ajeitá-la pra compararmos com o gráfico e tirar algumas conclusões, se liga:

Δ t = γ Δ t ' + Δ x ' u γ c 2

Se compararmos essa equação com o gráfico, podemos ver que Δ t e Δ x ' são linearmente dependentes. Ou seja, a relação entre os dois tem essa cara:

Δ t = a Δ x ' + b

Onde a e b são os coeficientes angular e linear, respectivamente.

Vamos usar as informações do gráfico pra calcular os coeficientes.

Passo 2

  • Coeficiente angular a :

O coeficiente angular é dado pela inclinação da reta, logo, usando a escala do gráfico:

a = 6 - 2 400 - 0 = 10 - 2 μ s / m

a = 10 - 8   s / m

Onde, de acordo com a equação:

a = u γ c 2

Beleza, daqui vamos conseguir (com um certo trabalho) calcular a velocidade u . Então, partiu! #fénopai #queoinimigocai

10 - 8 = u γ 3 × 10 8 2

u γ = 9 × 10 8

Substituindo a expressão de γ , teremos:

u 1 - u 2 c 2 = 9 × 10 8

1 1 u 1 - u 2 c 2 = 9 × 10 8

1 1 u 2 - 1 c 2 = 9 × 10 8

Elevando os dois lados ao quadrado:

1 1 u 2 - 1 c 2 = 8,1 × 10 17

1 u 2 - 1 c 2 = 1,23 × 10 - 18

1 u 2 = 1,23 × 10 - 18 + 1 3 × 10 8 2

1 u 2 = 1,23 × 10 - 17

Finalmente:

u = 2,85 × 10 8   m / s

Eu sei... foi chato demais.

Passo 3

Agora podemos determinar o fator de Lorentz, através da equação:

γ = 1 1 - u c 2

Substituindo os valores das velocidades:

γ = 1 1 - 2,85 × 10 8 3 × 10 8 2

γ = 3 , 2

Passo 4

Voltando para a transformação de Lorentz:

Δ t = γ Δ t ' + Δ x ' u γ c 2

Pra simplificar os cálculos, vamos escolher no gráfico o ponto em eu Δ x ' = 0 e Δ t = 2,0   μ s . Logo:

Δ t = γ Δ t ' → Δ t ' = Δ t γ

Substituindo os valores, teremos:

Δ t ' = 2 × 10 - 6 3,2

Δ t ' = 6,25 × 10 - 7 s

Resposta

Δ t ' = 6,2 5 × 10 - 7 s

Exercícios de Livros Relacionados

65 . Suponha que nosso Sol esteja para explodir. Em um esforço para fugir, partimos em uma espaçonave com v=0,800 c em direção à estrela Tau Ceti, a 12,0 anos-luz de distância. Quando alcançamos a met
61. Um sistrema S ' possui um componente x da velocidade igual a u relativa um sistema S e para t = t ' = 0 os dois sistemas coincidem (Figura 37.3 ). Um pulso de luz é emitido na origem de S ' no ins
No quadro S, o evento B ocorre 2,0 μs após o evento A, e o evento A ocorre na origem, enquanto o evento B ocorre no eixo x em x = 1,5 km. Com que velocidade e em que direção um observador deve estar v
A equação para a frente de onda esférica de um pulso de luz que começa na origem no tempo t = 0 é x2 + y2 + z2 - (ct) 2 = 0. O quadro S ′ se move com velocidade v ao longo do eixo x. Usando a transfor
Uma longa haste paralela ao eixo x é liberada do repouso. Subsequentemente, ele está em queda livre com uma aceleração de magnitude g na direção –y. Um observador em um foguete se movendo com velocida