Transformada de Lorentz para a Velocidade
Teoria
Novamente, o sistema de referência se move em relação a um segundo sistema de referência com velocidade na direção .
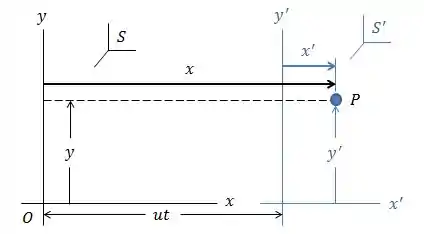
Por definição, a velocidade no referencial é dada por:
A partir das Transformações de Lorentz pra Espaço e Tempo podemos dizer que:
Daqui, fazendo a divisão e organizando os termos direito, o que vamos encontrar é o seguinte:
Podemos usar exatamente o mesmo raciocínio para calcular todas as outras velocidades, por exemplo:
Mas pra não quebrarmos ainda mais a cabeça com isso, vou te colocar na boa:
- Transformação de (em repouso) para (em movimento):
- Transformação de (em movimento) para (em repouso):
Novamente, nas situações em que , , e as Transformações de Lorentz se tornam as transformações de Galileu.
Obs.: Você precisa tomar cuidado pra não confundir as velocidades e , por exemplo. A velocidade é a velocidade com a qual o referencial se move em relação ao referencial . Enquanto a velocidade é a velocidade no eixo de um evento observado no referencial e é a velocidade no eixo de um evento observado no referencial .
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 179-29.
Uma partícula está se movendo ao longo do eixo do referencial com uma velocidade . O referencial está se movendo com uma velocidade de em relação ao referencial . Qual é a velocidade da partícula no referencial ?
Passo 1
O enunciado nos deu a velocidade da partícula no referencial e a velocidade relativa entre os dois referenciais. Agora já podemos nos virar sozinhos.
A velocidade da partícula no referencial será dada por:
Onde:
Substituindo esses caras na expressão da velocidade, teremos:
Ou:
Resposta
Exercício Resolvido #2
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, cap 37.
Duas partículas são produzidas em um acelerador de partículas de alta energia e se afastam em sentidos opostos.
A velocidade de uma das partículas, medida no laboratório, é igual a , e a velocidade relativa entre as duas é de .
Qual é o módulo da velocidade da outra partícula, medida no laboratório?
Passo 1
Vamos começar identificando os nossos referenciais em repouso e em movimento .
Nesse caso, o nosso referencial em repouso é o laboratório, e vamos adotar o nosso referencial em movimento como sendo uma das partículas em movimento.
Assim, o problema já nos diz o valor da velocidade entre os dois referenciais e, quando ele diz “velocidade relativa”, na verdade já está nos dizendo a velocidade medida no referencial em movimento , nesse caso, .
Passo 2
Trata-se de um problema de Transformações de Lorentz para a velocidade.
Como queremos determinar a velocidade da outra partícula em relação ao laboratório (referencial em repouso), queremos calcular , dado por:
Vale lembrar que, como as duas partículas estão se deslocando em sentidos opostos, vamos adotar que possui um sinal negativo (se deslocando no sentido negativo do eixo ), e que possui sinal positivo (se deslocando no sentido positivo do eixo ).
Passo 3
Onde:
;
;
Logo:
Resposta
Exercício Resolvido #3
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, cap 37.
Uma espaçonave da Armada Imperial se desloca com velocidade elevada em relação ao planeta Arrakis e dispara um foguete na direção do planeta com uma velocidade de em relação à espaçonave.
Um observador na superfície da Arrakis verifica que o foguete está se aproximando com velocidade de .
Qual é a velocidade da espaçonave em relação ao planeta Arrakis?
A espaçonave está se aproximando ou se afastando de Arrakis?
Passo 1
Vamos começar identificando os nossos referenciais em repouso e em movimento .
Nesse caso, o nosso referencial em repouso é o planeta Arrakis, e o nosso referencial em movimento é a espaçonave que dispara o foguete.
Assim, o problema já nos diz o valor da velocidade do foguete em relação à espaçonave , medida no referencial em movimento , e a velocidade medida no referencial em repouso , nesse caso, .
Passo 2
Trata-se de um problema de Transformações de Lorentz para a velocidade.
Como queremos determinar a velocidade entre a espaçonave e o planeta Arrakis, queremos calcular . Para isto, podemos usar a seguinte equação.
Nesse caso, vamos supor que tanto a espaçonave quanto o foguete estão se deslocando no mesmo sentido. Assim, adotaremos o mesmo sinal para ambas as velocidades (positivo).
Se no final das contas o valor que acharmos para for positivo, significa que a nossa hipótese está correta. Se o valor de for negativo, significa que, a espaçonave está, na verdade, se afastando do planeta, ok?
Passo 3
Onde:
;
;
Logo:
Reforçando o que dissemos anteriormente quando fizemos a nossa hipótese, como achamos um valor negativo para , significa que, na verdade, a nave está se afastando do planeta Arrakis.
Resposta
;
A espaçonave está se afastado de Arrakis;
Exercício Resolvido #4
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, cap 37.
Uma nave do planeta Tatooine está tentando alcançar um cruzador da Federação do Comércio. Em relação a um observador em Tatooine, o cruzador está se afastando do planeta com uma velocidade de .
A nave está se deslocando com uma velocidade de em relação a Tatooine, no mesmo sentido que o cruzador.
- Para a nave alcançar o cruzador, a velocidade do cruzador em relação a ela deve ser positiva ou negativa?
- Qual é a velocidade do cruzador em relação à nave?
Passo 1
a) Para a nave alcançar o cruzador, a velocidade do cruzador em relação a ela deve ser positiva ou negativa?
Para que a nave alcance o cruzador, é necessário que, do referencial da nave, o cruzador esteja se aproximando.
Ou seja, a velocidade do cruzador em relação à nave deve ser negativa, considerando positivo o sentido em que o cruzador e a nave se movem em relação ao planeta Tatooine.
Passo 2
b) Qual é a velocidade do cruzador em relação à nave?
O primeiro passo é sempre definir quem são os referenciais em repouso e em movimento.
Nesse caso, estamos interessados em descobrir a velocidade do cruzador em relação à nave.
Assim, a nave é o nosso referencial em movimento e o planeta Tatooine é o nosso referencial em repouso .
Passo 3
Trata-se de um problema de Transformação de Lorentz para a velocidade.
O problema nos dá a velocidade da nave em relação ao planeta (referencial em repouso), e a velocidade do cruzador em relação ao planeta.
Portanto, para encontrarmos a velocidade do cruzador em relação à nave (referencial em movimento), temos que fazer uma transformação do referencial (em repouso) para o referencial (em movimento), dada por:
Passo 4
Onde:
;
;
Logo:
Resposta
a)
Negativa.
b)