Conservação do Momento Linear
Produzido por Ludovic BeghinTeoria
Fala aí, seja bem vindo ao Responde Aí! Bora conversar sobre a conservação do momento linear?
Lei da Conservação do Momento Linear
O momento linear é dado por:
Onde
📢 Clique para ver mais:
Conservação do Momento Linear: Exemplo
Vamos ver um exemplo pra entender o que rola nesses casos. Uma pessoa de massa
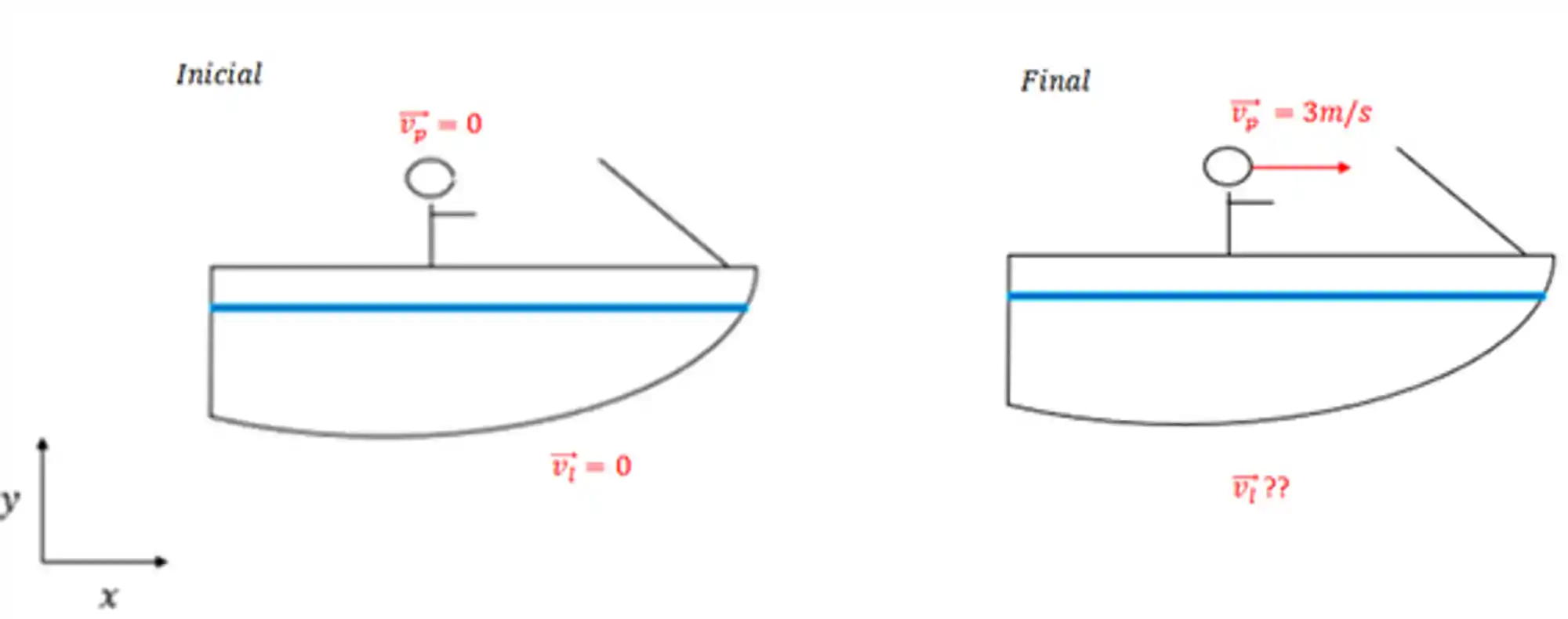
O momento linear de um sistema é conservado se o somatório das forças externas ao sistema for nulo, como é o nosso caso do sistema lancha + pessoa e vamos desenhar o diagrama de corpo livre para analisar melhor isso:
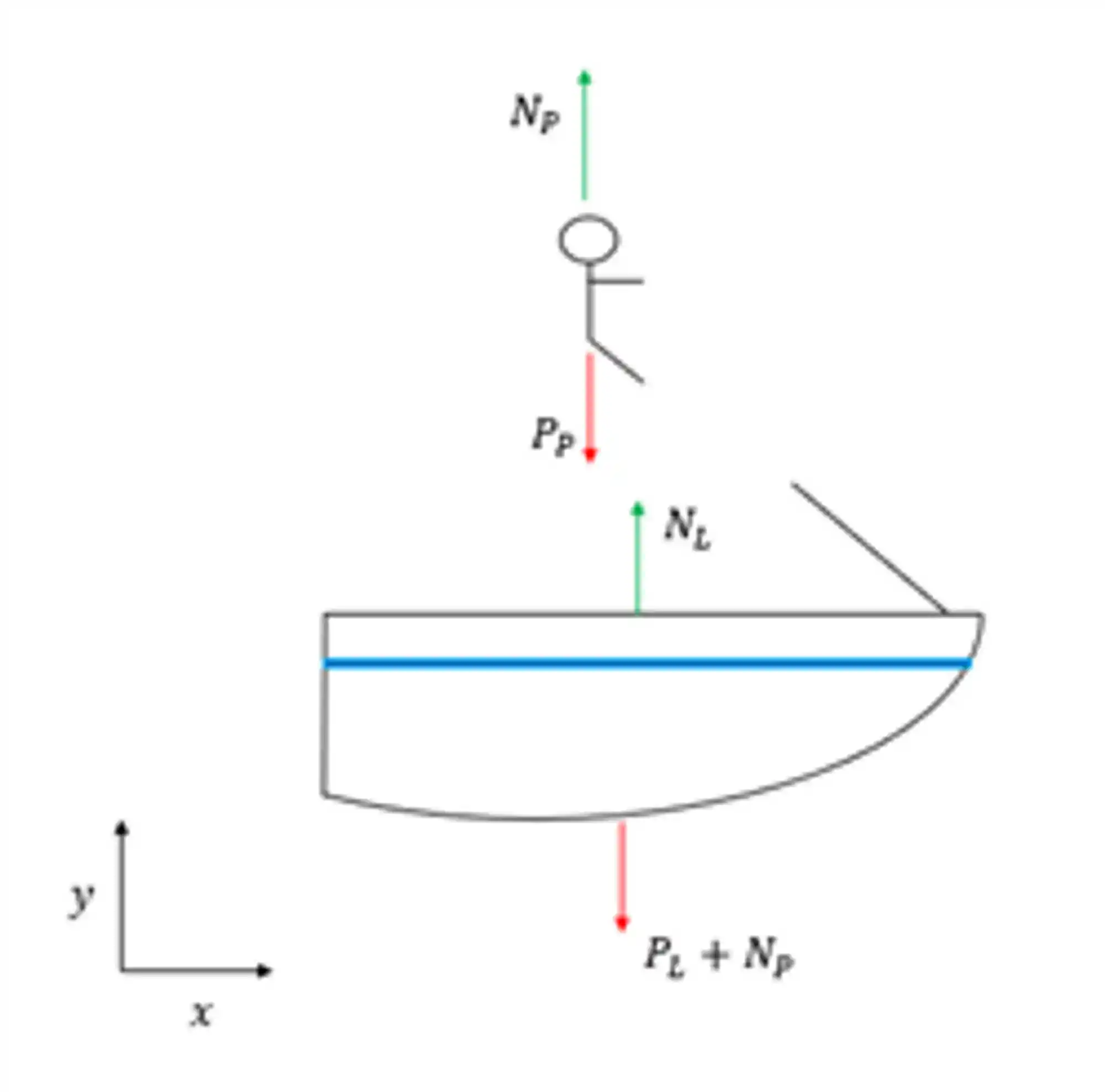
E aqui como o somatório das forças é zero o momento linear do sistema se conserva, e aí:
Considerando para direita como sendo o nosso positivo, escrevemos que:
E a gente pode fazer algumas considerações aqui pra facilitar a vida, a velocidade inicial da lancha é
Isolando a velocidade da lancha temos:
Substituindo os dados, temos:
Ou seja, a pessoa andou para um lado e a lancha para o outro e isso acontece pra que o momento linear do sistema se conserva!
Colisões
No caso das colisões, as únicas forças que atuam são forças internas do sistema, e por isso, em uma colisão vai haver sempre a conservação do momento linear. Imagina que você tá lá jogando sinuca com seus amigos e cada bolinha possui massa
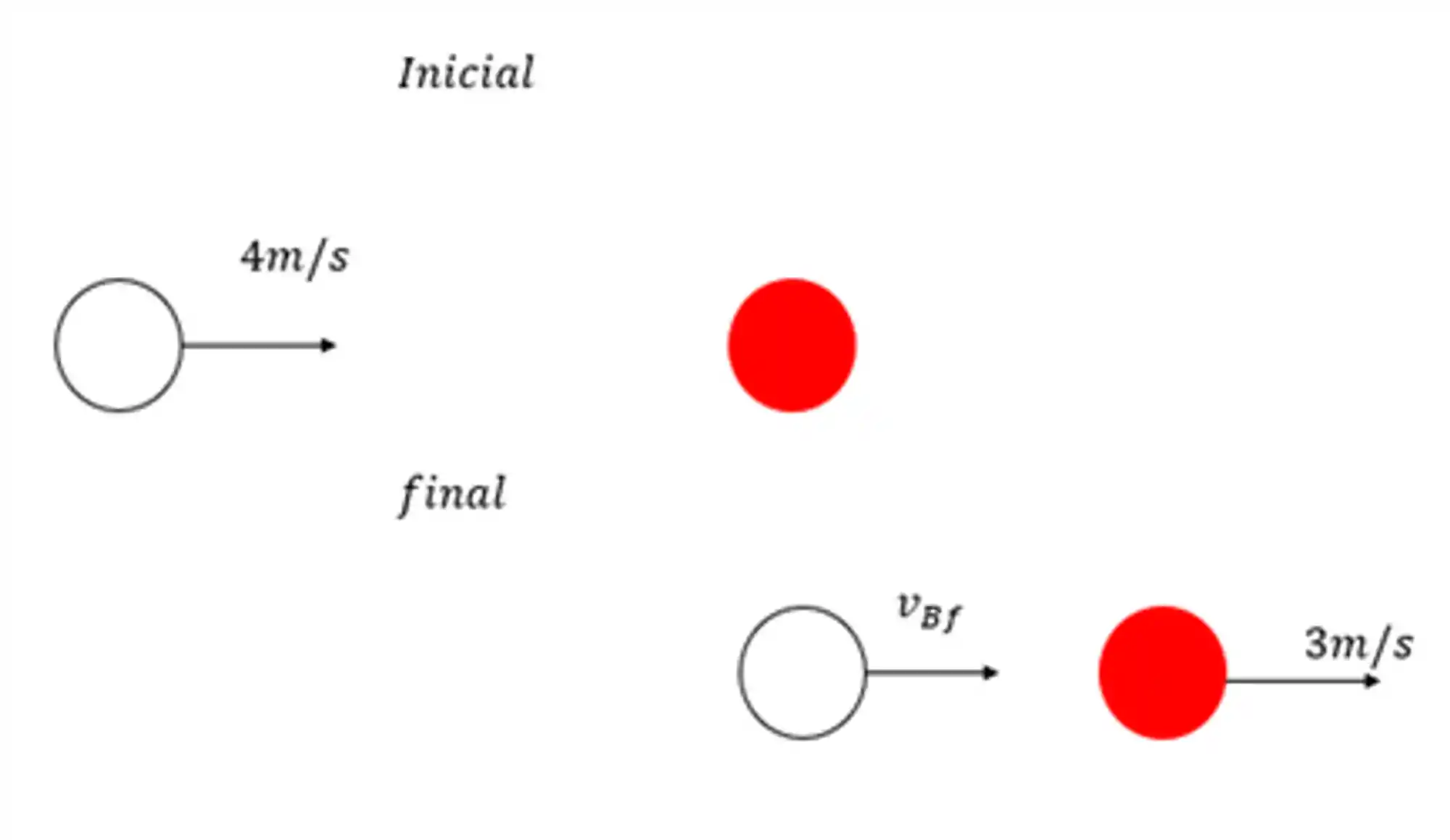
No exemplo acima qual é a velocidade final da bola branca?
Vamos entender primeiro porque o momento linear pode se conservar nesse caso, o impulso foi inserido no sistema pelo taco antes do estado inicial considerado e se manteve o mesmo, outro ponto é o somatório de forças que é nulo e pra isso a gente pode desenhar o diagrama de corpo livre das bolinhas.

Onde
Dessa forma temos:
Como a massa das bolas é igual, podemos cortar dos dois lados da equação:
E isolando a velocidade final da bola branca e substituindo os valores, temos:
O momento linear se conserva pra qualquer tipo de colisão, e a gente vai estudar isso melhor mais pra frente, beleza?
Você também pode conferir esse conteúdo em vídeo:
Independência dos eixos
O momento linear é um vetor e com isso, quando vamos conserva-lo, ficamos com:
Mas e se o nosso problema for bidimensional, ou tridimensional. Como ficamos? Nesse caso podemos dizer que:
Onde os eixos
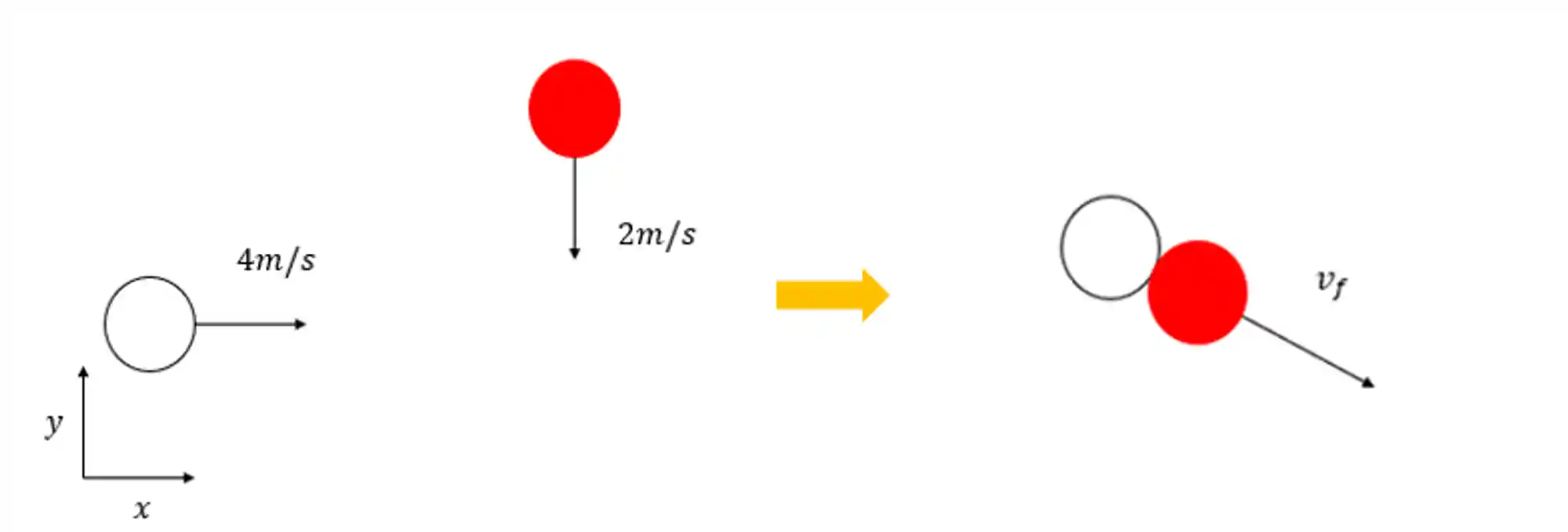
Nesse exemplo, as bolinhas se engataram e passaram a se mover juntas então temos a conservação de momento. Dessa forma elas passam a ser um sistema e a andar juntas com a mesma velocidade final.
Agora resolvemos o problema considerando cada eixo individualmente:
Para o eixo X
Para o eixo Y
Assim, nós encontramos as componentes horizontal e vertical da velocidade final. Também podemos escrevê-la vetorialmente:
Algo interessante na independência dos eixos é que pode haver casos que o momento se conserva em um eixo, mas não se conserva em outro. Por exemplo quando o vetor impulso
Agora vamos praticar com exercícios?
Colisões
Independência dos eixos
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp – 253-16
Você está em pé sobre uma camada de gelo de um estádio de futebol em um país frio: despreze o atrito entre seus pés e o gelo. Um amigo joga para você uma bola de 0,400 kg que se desloca horizontalmente com velocidade de . Sua massa é igual a . Se você agarra a bola, com que velocidade você e a bola se deslocarão logo a seguir? Se a bola colide com você e rebate em seu peito, passando a adquirir uma velocidade horizontal de em sentido oposto ao inicial, com que velocidade você se desloca após a colisão?
Passo 1
O Sistema tratado no problema é a bola e você, onde
O problema faz questão de nos pedir para ignorar o atrito, e isso nos permite dizer que não a ação de forças externas no sistema, logo o momento liner do sistema vai se conservar.
Passo 2
Você agarrou a bola, qual a velocidade final sua? Pela conservação d emomento podemos dizer que
O momento linear inicial é
Passo 3
O momento linear final é
Como você agarrou a bola, isso significa que vocês estão juntos, logo com a mesma velocidade final
Passo 4
Aplicando a conservação de momento linear temos
Achou estranho uma velocidade tão baixa? Relaxa, que está certo, como sua massa é muito superior a massa da bola para os momentos serem iguais a velocidade sua e da bola tem que ser bem pequena mesmo.
Passo 5
Isso nada mais é que o choque de dois objetos, certo? Então o momento linear conserva.
O momento inicial já temos
O momento final que vai mudar, pois agora a bola rebate e volta com módulo e sinal da velocidade diferente
A velocidade final da bola é
É negativa por ser no sentido contrário a velocidade inicial.
Então,
Aplicando a conservação de momento linear, temos que
Resposta
Exercício Resolvido #2
PUC-RIO – 2ª Prova – 2014.2
Um carrinho de massa move-se em linha reta sobre um piso horizontal sem atrito com velocidade de . Sobre o carrinho encontra-se fixada na posição horizontal, uma mola que é comprimida por um bloco de massa . Inicialmente, o bloco se encontra preso ao carrinho por um fio comprimindo a mola. Em certo instante, o fio se rompe e a mola empurra o bloco para fora do carrinho, projetando-o com uma velocidade de em relação ao piso. Uma vez livre do bloco, qual a nova velocidade do carrinho?
Passo 1
Não há forças externas aplicadas na direção do movimento do sistema e as forças internas relacionadas entre o bloco e o carrinho são produzidas em pares ação e reação, se anulando mutuamente, ocorrendo assim conservação do momento linear total do sistema.
Vamos analisar quem eram as componentes do sistema antes, e depois e então calcular o momento linear usando:
Após isso igualaremos os momentos lineares antes e depois e acharemos a nova velocidade do carrinho.
Passo 2
O sistema inicialmente era composto por carrinho + bloco juntos andando na mesma velocidade, sendo assim temos pro caso inicial:
A massa do carrinho:
A massa do bloco:
A velocidade dos dois andando em conjunto:
Sendo assim podemos dizer que o momento linear inicial é:
E aqui podemos tirar a notação vetorial já que o enunciado nos mostra que a velocidade final será no mesmo eixo.
Passo 3
Agora vamos analisar o caso final por aqui. Após o rompimento do fio, a mola se estica e joga o bloco pra fora com velocidade , no sentido oposto da velocidade anterior no eixo . Agora que o esquema tá separado cada um anda com uma velocidade diferente, vamos escrever isso aqui:
Substituindo os valores das massas e da velocidade temos:
Agora é só a gente aplicar a conservação do momento linear né:
Então é a letra e)
Resposta
Letra
Exercício Resolvido #3
PUC-RIO – 2ª Prova – 2009.2- letra b- Modificado
Vamos supor que duas partículas e colidem bidimensionalmente. Seja a partícula de massa e a partícula de massa . As posições das partículas num certo instante antes da colisão são dadas por e . O tempo de duração da colisão é de .
Suponha agora que as velocidades no início da colisão são: e , e que no fim da colisão a componente da velocidade de é igual a e a componente da velocidade de é . Escreva os vetores velocidade de ambas as partículas no fim da colisão.
Passo 1
Pela conservação do momento linear no início e no fim da colisão:
Onde e e e . Então:
Como podemos separar a equação da conservação de momento linear por eixos temos
Assim:
E
Resposta
;
Exercício Resolvido #4
UFF – 2ª Prova – 2014.1
Dois automóveis viajam em duas estradas perpendiculares entre si, colidem e ficam juntos após a colisão. O carro tem massa de e tinha velocidade de antes da colisão. O carro tem massa de . As marcas de derrapagem dos carros juntos, imediatamente após a colisão fazem um ângulo de com a direção inicial do carro . Qual era a velocidade do carro antes da colisão?
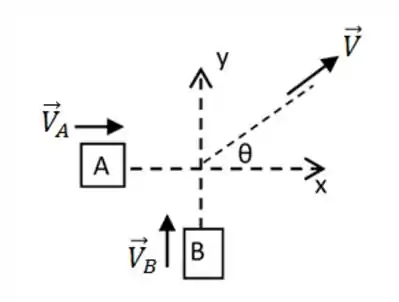
Passo 1
Esse é um problema de conservação de momento linear em duas direções, e a primeira coisa que a gente tem que fazer é pensar no que acontece antes e no que acontece depois da colisão, anotando cada dado.
Após isso vamos aplicar a conservação do momento linear, podemos fazer vetorialmente que o momento linear inicial é igual ao final.
Ou separando por eixos.
Esse segundo jeito é mais fácil de visualizar um pouco, vamos fazer assim tá? Lembrando que:
Passo 2
Vamos analisar o que acontece antes da colisão: O carro tem massa e anda para a direita, ou sentido positivo de com velocidade . Já o carro possui massa e velocidade que queremos descobrir indicada no sentido positivo de , ou seja, pra cima . Se liga aí no desenho:
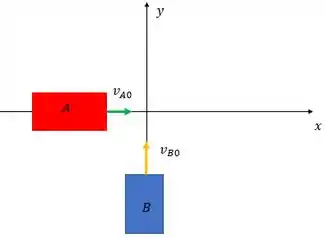
Sendo assim o momento linear desse sistema antes da colisão é em cada eixo:
Repara que o carro não tem momento linear na horizontal e o carro não tem momento linear na vertical, isso aí acontece por quê a velocidade desses carros nesses eixos é 0.
Vamos partir pra analisar o que acontece depois da colisão, ok?
Passo 3
Depois da colisão temos a seguinte situação: os carros e formam um sistema que anda junto, sendo assim a massa desse sistema é:
Esse sistema anda com velocidade final que não conhecemos e essa velocidade está angulada de em relação ao eixo. Se liga nesse desenho aí, pra gente entender legal:
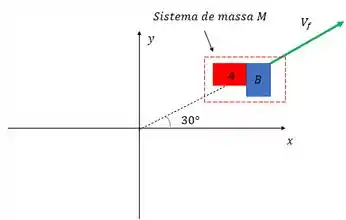
E aqui vai o bizu da questão, essa velocidade final deve ser decomposta nos dois eixos pra gente poder analisar separado cada momento linear. Podemos decompor ela da seguinte forma:
Então temos pros casos finais os seguintes momentos lineares:
E para o eixo :
Bacana, nosso próximo passo será aplicar a conservação do momento linear para cada eixo.
Passo 4
Vamos então aplicar essa conservação do momento linear, mas aqui precisaremos seguir uma lógica. Temos duas incógnitas e , vamos primeiro precisar encontrar e o jeito é começar analisando a conservação no eixo .
E aqui é substituir os valores que encontramos para cada um desses momentos lineares:
Isolando temos:
Bacana né, agora é só fazer isso pro outro eixo substituindo o valor de
Ufa, encontramos essa velocidade! Mais um exercício resolvido 😊.
Resposta
Exercício Resolvido #5
PUC-RIO – 2ª Prova – 2009.1
Uma nave viaja no espaço com vetor velocidade relativa a um observador, contendo uma carga. A massa total do sistema é . Em certo momento a nave libera a carga (massa ) com vetor velocidade relativa ao mesmo observador. Encontre uma expressão para o novo vetor velocidade da nave se durante a liberação da carga.
Passo 1
Já que não há forças externas atuando, podemos aplicar a conservação do momento linear total! O momento linear do sistema é igual antes e depois da nave soltar a carga:
Passo 2
No começo a nave e sua carga estão juntas, tendo uma massa total e andando com uma velocidade . Então o momento linear total é
Passo 3
Depois da nave soltar a carga, o sistema passa a ter 2 partículas, a nave de massa e andando a uma velocidade e a carga de massa a uma velocidade , então
Passo 4
Aplicando a conservação do momento linear total:
Pronto, é só isso! :)
Resposta
Exercício Resolvido #6
UFRJ – 2ª Prova – 2012.1
Uma partícula de momento , projétil, colide não frontalmente, isto é, colide bidimensionalmente, com uma outra partícula, inicialmente em repouso, que chamamos de alvo. Após a colisão o projétil tem momento e o alvo sai com momento . A conservação do momento linear, neste processo é corretamente representado pelo diagrama:
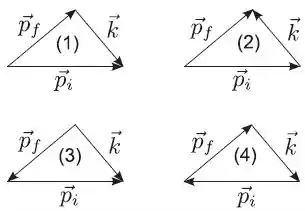
Nenhum diagrama está correto
Passo 1
O momento linear nesse problema é conservado e fica escrito como
Vamos considerar que o momento linear só tem componente horizontal, como está desenhado em todos os diagramas.
Os vetores e tem componentes verticais, mas eles são contrários já que a soma das suas componentes deve ser zero. Isso exclui o diagrama e o diagrama
Passo 2
Além disso a soma das suas componentes horizontais deve ser igual a componente horizontal de .
Somando e como indicado nos diagramas vamos ter
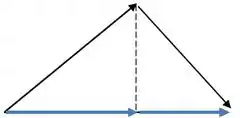
A componente horizontal da soma vai ser para direita, então o momento linear também deve ser para direita.
Resposta
Letra
Exercício Resolvido #7
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp – 253
O bloco indicado na figura abaixo possui massa igual a , e o bloco possui massa igual a . Os dois blocos se aproximam, comprimindo a mola entre eles; a seguir o sistema é libertado a partir do repouso sobre uma superfície horizontal sem atrito. A mola possui massa desprezível, não está presa a nenhum dos blocos e cai sobre a mesa depois que ela se expande. O bloco adquire uma velocidade de . Qual a velocidade final do bloco ? Qual foi a energia potencial armazenada na mola comprimida?
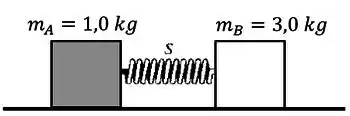
Passo 1
Nesse exercício vamos considerar o sistema como os dois blocos e a mola.
Quando eles comprimem a mola, a força elástica vai ser igual nos dois blocos, tendo resultante zero.E como não há ação de forças externas no sistema, isso quer dizer que o momento linear do sistema se conserva
Diferente do normal eu escrevi sem ser na forma vetorial, repara que só vamos ter movimento ao longo da horizontal então o movimento é unidimensional, não preciso usar vetores.
Passo 2
Vamos considerar o momento onde a mola está comprimida ao máximo(momento inicial), e depois o momento que os blocos descolam da mola (momento final).
Vamos considerar o sentido positivo do eixo sendo da esquerda para direita, assim é positivo.
Temos que o momento inicial é zero
Passo 3
Como o momento se conserva temos que o momento final também deve ser zero
Vamos então calcular o momento linear final
Como sabemos que o momento linear final é zero, temos
Passo 4
Como não temos forças dissipativas atuando, como o atrito, a energia mecânica do sistema se conserva
Como no inicio temos só a mola comprimida
E no final temos a mola relaxada e os blocos em movimento
Passo 5
Sendo assim
Resposta
Exercício Resolvido #8
USP-2015
Um bloco inicialmente em repouso explode em dois pedaços que entram em regiões com atrito onde terminam parando. O primeiro pedaço possui massa de 2 kg se move para a esquerda até parar após percorrer uma distância de 0, 15 m. O segundo pedaço se move para a direita e pára após percorrer uma distância de 0, 25 m. Sabendo que os coeficientes de atrito nas duas regiões são iguais, a massa total do bloco vale aproximadamente:
Passo 1
Temos uma situação em que a caixa explode,indo pra uma parte pra um lado e outra pro outro, como na figura abaixo:
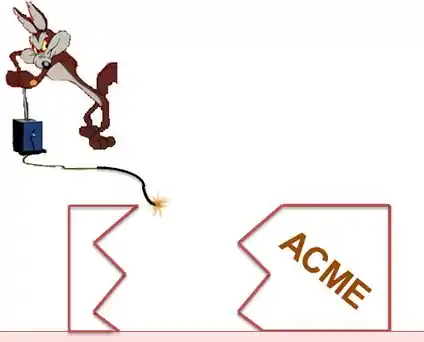
Só aqui já podemos perceber que:
- O momento se conserva (não há ação de forças externas);
- A força resultante na direção do deslocamento será apenas o atrito;
- A energia mecânica adquirida será gasta pelo trabalho da força de atrito.
Passo 2
Chamando a massa do primeiro bloco de e a velocidade adquirida após a explosão de , e a massa do segundo bloco (o escrito ACME) de e a velocidade , teremos, pela conservação do momento:
Como só teremos movimento em uma direção, podemos desconsiderar os vetores e só usar a parte escalar:
Como antes tava tudo parado, , teremos:
Passo 3
Sendo agora as distâncias percorridas até parar respectivamente do bloco “1” e do “2” e o coeficiente de atrito, a gente vai ter, pelo Teorema Trabalho- Energia Cinética:
O trabalho da força de atrito é dada por:
Para o bloco 1, teremos:
Para o bloco 2 é só fazer a mesma coisa...
Passo 4
Divindo a equação de 1 pela de 2, vai ficar:
Mas lááá do “Passo 1”, temos que a relaçãozinha:
Passo 5
Vamos fazer assim, pega o e divide por e isola a fração. Tipo assim:
Eleva aí os dois lados ao quadrado aí fica...
Passo 6
Mas oh, lá no “Passo 4” a gente viu que
Substituindo no que acabamos de ver:
Como a gente sabe, , e
Substituindo lá...
Como a mossa total da caixa é dada por:
Vamos ter que:
Resposta
Letra
Exercício Resolvido #9
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp – 258
João e José estão sentados em um trenó que está inicialmente em repouso sobre uma superfície de gelo sem atrito. O peso de João é igual a , o peso de José é igual a e o peso do trenó é igual a . Ao notar a presença de uma aranha venenosa no interior do trenó eles imediatamente pulam para fora. João pula para a esquerda com velocidade (em relação ao gelo) igual a formando um ângulo de acima da horizontal, e José pula para direita com velocidade (em relação ao gelo) igual a formando um ângulo de acima da horizontal. Determine o módulo, a direção e o sentido da velocidade do trenó depois que eles pulam para fora.
Passo 1
Estamos em um caso novamente onde vamos usar a conservação do momento linear para o sistema. Porque ele se conserva? Porque a soma das forças externas na horizontal é zero, o sistema João-José-Trenó está em repouso no início, ou seja, em equilíbrio.
Devemos então fazer
Passo 2
No início como todos estão em repouso
Vamos fazer um esquema de como é são as velocidades após eles pularem.

Devemos então escrever cada velocidade na forma vetorial, usando a “regra do COlado/SEparado”
Passo 3
Para a velocidade do José
Passo 4
Para a velocidade do João
Passo 5
Calculando o momento linear do sistema após o pulo
Sabemos que
Então
No enunciado, ele não nos dá a massa, mas sim o peso. Vamos multiplicar essa equação pela gravidade e repara num detalhe
Agora basta substituir os dados do enunciado
Na realidade a componente da velocidade do trenó é zero. Isso porque na vertical a força normal gera um impulso no trenó que mantém ele parado.
Então a velocidade do trenó só tem componente horizontal que calculamos
Escrevendo na forma vetorial
Como a componente é zero, o módulo é o memso valor da componente
Resposta
;