Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Posição do Centro de Massa

Ver Todos os Exercícios

Teoria

Bora aprender o que é um Centro de Massa e como calculá-lo?!

O que é o Centro de Massa?

O centro de massa é o ponto onde podemos concentrar toda a massa do corpo e entender ele como se fosse uma partícula pontual onde o tamanho não importa.

Pra entender melhor como funciona esse tal de centro de massa e como calculá-lo, confere esse vídeo super completo que o Responde Aí preparou pra você! 👇

📢 Clique para saber mais:

Centro de Massa em um Sistema de Partículas

A posição do centro de massa de um sistema é dado pela média ponderada da posição dos objetos no sistema, onde o peso é a massa de cada objeto. A fórmula para a posição do centro de massa é:

Onde , representam as posição do centro de massa do objeto respectivamente.

Bora aprender na prática como calcular o centro de massa?! Se liga no exemplo abaixo:

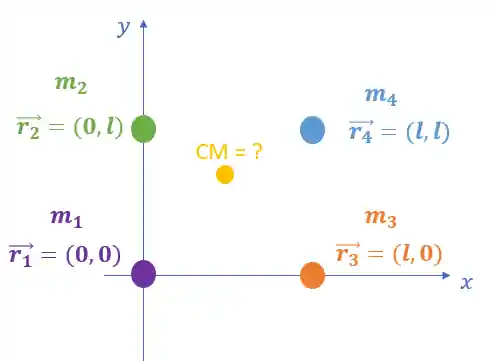
Centro de Massa de um sistema de partículas
Centro de Massa de um sistema de partículas

Onde , e .

O vetor posição do centro de massa será igual a:

Calculando, temos:

O centro de massa de figuras simétricas como esferas, círculos, quadrados, retângulos é o ponto central da figura. Por exemplo, se o sistema que apresentamos anteriormente tivesse todas as massas iguais e em posições simétricas, o centro seria no centro do quadrado formado pelas partículas:

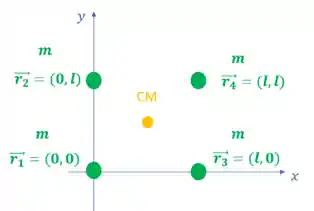
Centro de massa de sistemas simétricos
Centro de massa de sistemas simétricos

Poderíamos escrever o vetor posição do centro de massa:

A simetria é um dado importante, sempre que houver um eixo de simetria em um sistema o centro de massa estará nesse eixo de simetria.

Como achar o Centro de Massa de um corpo?

Em objetos homogêneos, isso é, com densidade constante, o centro de massa do objeto será igual o seu centro geométrico.

Por exemplo, o centro de massa de um disco será o centro do disco:

centro de massa de um disco
centro de massa de um disco

O centro de massa de um fio de comprimento será :

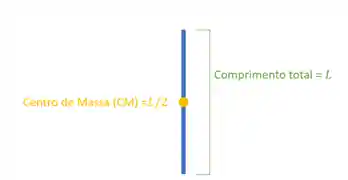
centro de massa de um fio
centro de massa de um fio

Centro de Massa de um Corpo com Furo

Como faz pra calcular a posição do centro de massa de um corpo com furo?

Centro de Massa de um Corpo com Furo
Centro de Massa de um Corpo com Furo

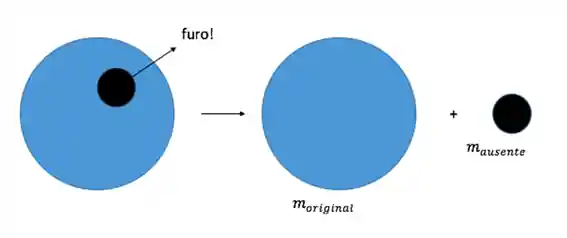
Vamos tratar o problema da seguinte forma. O sistema será composto por dois objetos:

  • O “corpo original” ( o corpo sem furo) de massa ;
  • O “corpo ausente” de massa .

Calcularemos a posição do centro de massa da mesma forma:

Agora vamos praticar com exercícios?!

Centro de Massa em um Sistema de Partículas

Como achar o Centro de Massa de um corpo?

Centro de Massa de um Corpo com Furo

Exercícios Resolvidos

Exercício Resolvido #1

UERJ – 2ª Lista

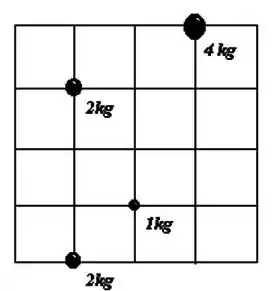
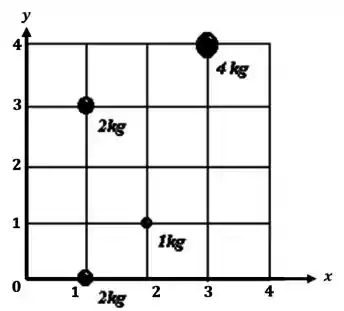
Calcule o centro de massa do objeto esquematizado na figura abaixo (despreze a massa da grade):

Passo 1

O primeiro passo é escolher um referencial e um sistema de medida. Vamos adotar aqui que os lados de cada quadrado da grade valem 1u.

Passo 2

Agora precisamos da posição de cada um dos objetos.

Temos a posição r → 1 = ( 2,1 ) para o objeto de massa 1   kg .

Temos as posições r → 2 = ( 1,0 ) e r → 3 = ( 1,3 ) para os objetos de massa de 2   kg .

Temos a posição r → 4 = 3,4 para o objeto de massa 4   kg .

Passo 3

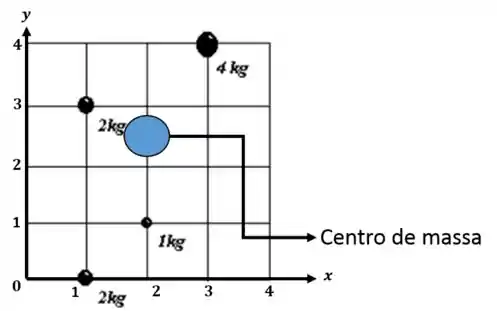
Agora é só aplicar a fórmula para achar a posição do centro de massa.

r → C M = m 1 r → 1 + m 2 r → 2 + m 3 r → 3 + m 4 r → 4 m 1 + m 2 + m 3 + m 4

r → C M = 1 2 ,   1 + 2 1 ,   0 + 2 1 ,   3 + 4 ( 3 ,   4 ) 1 + 2 + 2 + 4

r → C M = ( 18 ,   23 ) 9

r → C M = 2 , 23 9

Agora podemos ilustrar onde está o centro de massa.

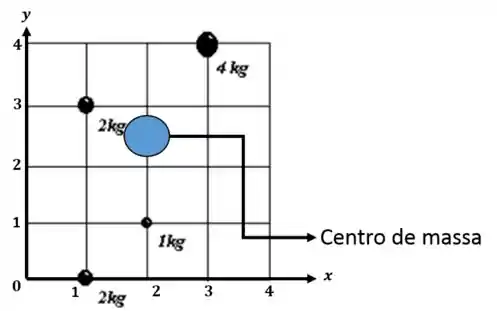
Resposta

r C M → = 2 , 23 9

Exercício Resolvido #2

UFRJ-P2-2015.1- ME3

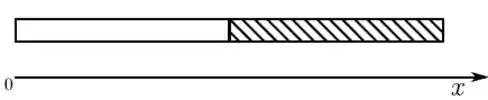
Uma barra de comprimento 2 L é formada por duas metades, como mostra a figura. A parte da esquerda possui metade da massa da parte da direita, hachurada. Separadamente, as duas partes são homogêneas. Desejamos usar um fio para prender esta barra ao teto. Para que a barra fique em equilíbrio, na posição horizontal, ela deve ser pendurada pelo ponto x   tal que

(a) x = L

(b) x = 7 6   L

(c) x = 3 2 L

(d) x seja qualquer entre 0   e 2 L

(e) x seja qualquer entre L e 2 L

Passo 1

Para que a barra fique em equilíbrio, o fio tem que ser ligado ao centro de massa da barra.

O centro de massa é como se a massa estivesse concentrada naquele ponto. Portanto o peso atua naquele ponto, e para que não haja um torque e a barra rotacione, o fio é preso no centro de massa da barra, se for preso em outro ponto, o peso causará uma rotação na barra.

Passo 2

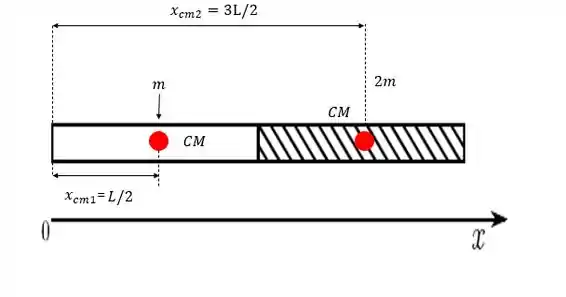
Então vamos achar a posição do CM da barra, e para isso faremos esse cálculo em relação a origem.

O comprimento da metade esquerda da barra é L , e ela é homogênea. Então o centro de massa dessa metade fica em x = L / 2 .

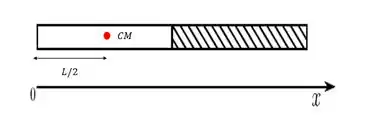
Digamos que a massa dessa metade é m . Então vamos considerar a massa m toda concentrada em x = L / 2 .

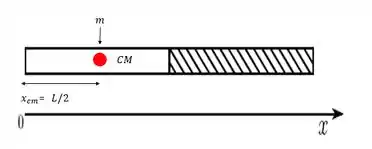
Pra outra metade podemos fazer a mesma coisa, a diferença é que a posição do CM é L + 2 L 2 = 3 L / 2 e que a massa é dobro, 2 m .

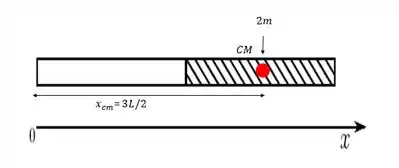
Sendo assim o nosso sistema da barra final vai ficar desse jeito:

Passo 3

Agora ficou mais fácil de calcular a posição x C M do centro de massa !

Ela é dada por:

x C M = m 1 x C M 1 + m 2 x C M 2 m 1 + m 2

Sendo assim vamos substituir as massas e os centro de massa encontrados para encontrarmos a posição do centro de massa da barra:

x C M = m L 2 + 2 m 3 L 2 m + 2 m

x C M = m L 2 + 6 m L 2 3 m = 7 m L 6 m

x C M = 7 L 6

Sendo assim o fio será colocado na posição 7 L / 6 , vamos desenhar?

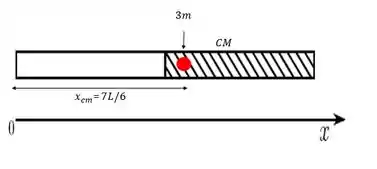
Então a resposta é b )

Resposta

Alternativa (b) 7 6 L

Exercício Resolvido #3

PUC-RIO – 2ª Prova – 2009.1

Considere a molécula d’água H 2 O com seus três átomos distribuídos com localizações fixas de acordo com a figura abaixo, sendo d a distância entre o átomo de Oxigênio ( O ) e um átomo de Hidrogênio ( H ) . Encontre o vetor posição do centro de massa da molécula, em relação à posição do átomo de Oxigênio, em função da distância d .

Sabe-se que θ = 105 o , cos ⁡ 15 o = 0,966 , sen ⁡ 15 o = 0,260 , m O = 16   u m a e m H = 1   u m a (unidades de massa atômica).

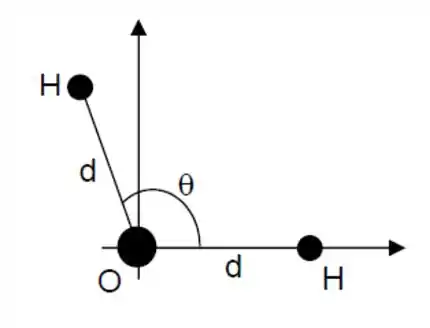
Passo 1

A primeira coisa que temos que fazer é deixar claro quais são nossos eixos!

Temos que calcular a posição do centro de massa do sistema em relação ao átomo de oxigênio O então O é a nossa origem. O eixo x aponta pra direita e o eixo y aponta pra cima.

Repare que as coordenadas do hidrogênio da direita são ( d , 0 ) . Vou chamá-lo de H 1 , ok?

Mas ainda precisamos achar as coordenadas do outro hidrogênio, o H 2 !

Passo 2

Sabemos que θ = 105 o então o ângulo entre o eixo y e o H 2 é 105 o - 90 o = 15 o . Não é à toa que deram pra gente cos ⁡ 15 o = 0,966 e sen ⁡ 15 o = 0,260 no enunciado!

Então queremos as coordenadas x H e y H do átomo de hidrogênio:

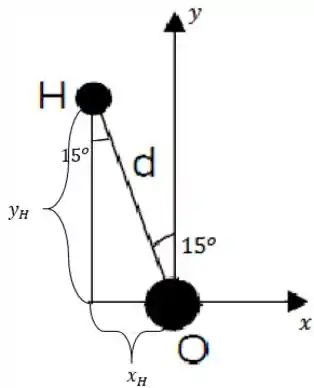
Olhando o triângulo formado na esquerda e aplicando trigonometria básica, temos:

x H = d sen ⁡ 15 o

y H = d cos ⁡ 15 o

Mas como o eixo x aponta pra direita, a coordenada x do átomo é - d sen ⁡ 15 o .

Passo 3

Vamos calcular a posição do centro de massa! :D

Recapitulando, as coordenadas dos 3 átomos são ( 0 ,   0 ) pro oxigênio, ( d ,   0 ) para o H 1 e - d sen ⁡ 15 0 ,   d cos ⁡ 15 o para o H 2 .

Vamos começar pela coordenada x do centro de massa:

x C M = m O x O + m H 1 x H 1 + m H 2 x H 2 m O + m H 1 + m H 2

m O = 16 e m H 1 = m H 2 = 1 , então isso dá

x C M = 16 ⋅ 0 + 1 ⋅ d + 1 ⋅ - d sen ⁡ 15 o 16 + 1 + 1

⇒ x C M = d - d sen ⁡ 15 o 18

⇒ x C M = 1 - sen ⁡ 15 o 18 d

Substituindo sen ⁡ 15 o = 0,26   isso dá:

x C M = 0,74 18 d ≈ 0,041 d

Passo 4

Show, agora vamos achar a coordenada y do C M !

y C M = m O y O + m H 1 y H 1 + m H 2 y H 2 m O + m H 1 + m H 2

⇒ y C M = 16 ⋅ 0 + 1 ⋅ 0 + 1 ⋅ d cos ⁡ 15 o 16 + 1 + 1

⇒ y C M = d cos ⁡ 15 o 18

Usando cos ⁡ 15 o = 0,966 temos

y C M = 0,966 18 d ≈ 0,054 d

Então é isso! Sendo i o vetor unitário do eixo x e j o vetor unitário do eixo y , o vetor posição do centro de massa da molécula, em relação à posição do átomo de oxigênio é:

r C M = 1 - sen ⁡ 15 o d 18 i ,     cos ⁡ 15 o d 18 j ≈ 0,041 d i ,   0,054 d j

Resposta

r C M = 1 - sen ⁡ 15 o d 18 i ,     cos ⁡ 15 o d 18 j ≈ 0,041 d i ,   0,054 d j

Exercício Resolvido #4

Elaboração Própria

Encontre a posição do centro de massa da chapa abaixo, considere a chapa homogênea.

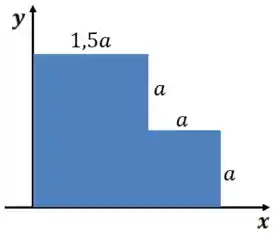
Passo 1

Essa chapa é o nosso sistema, podemos então “quebrá-la” em vários objetos que sabemos o centro de massa, mas quais são esses objetos? Retângulos, o centro de massa de retângulos é exatamente no seu meio. Separando essa figura temos

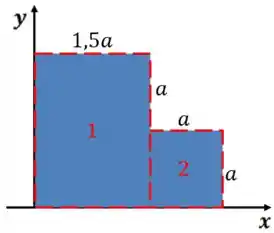
Vamos ter as seguintes componentes para o centro de massa dos retângulos (coordenadas do centro do retângulo):

r e t a n g u l o   1 x 1 = 1,5 a 2 = 0,75 a y 1 = 2 a 2 = a                        

r e t a n g u l o   2 x 2 = 1,5 a + a 2 = 2 a y 2 = a 2 = 0,5 a                

Passo 2

Quando cada objeto na verdade são chapas, podemos usar a área de cada uma delas em vez da massa, isso porque elas são proporcionais

Assim, vamos calculas a posição x do centro de massa

x C M = A 1 ⋅ x 1 + A 2 ⋅ x 2 A 1 + A 2

x C M = 1,5 a ⋅ 2 a ⋅ 0,75 a + a ⋅ a ⋅ 2 a 1,5 a ⋅ 2 a + a ⋅ a

x C M = 2,25 a 3 + 2 a 3 3 a 2 + a 2

x C M = 4,25 a 3 4 a 2

x C M = 1,0625 a

Passo 3

Agora, vamos calcular a posição y do centro de massa

y C M = A 1 ⋅ y 1 + A 2 ⋅ y 2 A 1 + A 2

y C M = 1,5 a ⋅ 2 a ⋅ a + a ⋅ a ⋅ 0,5 a 1,5 a ⋅ 2 a + a ⋅ a

y C M = 3 a 3 + 0,5 a 3 3 a 2 + a 2

y C M = 3,5 a 3 4 a 2

y C M = 0,875 a

Passo 4

O vetor centro de massa fica

r → C M = 1,0625 a i ^ + 0,875 a j ^

Resposta

r → C M = 1,0625 a i ^ + 0,875 a j ^

Exercício Resolvido #5

UFRJ – 2ª Prova – 2013.2

Uma chapa homogênea quadrada de lado 2 a tem um canto quadrado de lado a retirado. A chapa restante está disposta no plano O X Y como indicado na figura. Em relação à origem O , o vetor posição r → c m do centro de massa

a   7 / 6 a i ^ + j ^

b   5 / 6 a i ^ + j ^

c   1 / 3 a i ^ + j ^

( d )   1 / 2 a i ^ + j ^

e   2 / 3 a i ^ + j ^

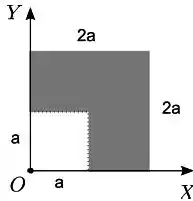
Passo 1

Tínhamos uma chapa quadrada de lado 2 a e então tiramos um pedaço quadrado de lado a da chapa. Ou seja, temos uma chapa com furo, assim podemos calcular a posição do centro de massa da figura pela fórmula

r → C M = r → o r i g i n a l . A o r i g i n a l   + r → b u r a c o . A b u r a c o A o r i g i n a l + A b u r a c o

Lembre-se também que quando temos chapas usamos sua área no lugar da massa.

Passo 2

Vamos ter as posições do centro de massa

C h a p a   o r i g i n a l x o r i g i n a l = a y o r i g i n a l = a → r → o r i g i n a l = a . i ^ + a . j ^

B u r a c o   x b u r a c o = a 2 y b u r a c o = a 2 → r → b u r a c o = a 2 . i ^ + a 2 . j ^

Além disso, temos as áreas

A o r i g i n a l = 2 a 2 = 4 a 2

A b u r a c o = - a 2  

A área do buraco é negativa, pois é um buraco, estamos representando a ausência de área na figura.

Passo 3

Pela fórmula do centro de massa vamos ter

r → C M = r → o r i g i n a l . A o r i g i n a l   + r → b u r a c o . A b u r a c o A o r i g i n a l + A b u r a c o

r → C M = a . i ^ + a . j ^ . 4 a 2 + a / 2 . i ^ + a / 2 . j ^ . - a 2 4 a 2 + - a 2

r → C M = 4 a 3 ( i ^ + j ^ ) - a 3 / 2 ( i ^ + j ^ ) 3 a 2

O vetor posição do centro de massa vai ser

r → C M = 7 a ( i ^ + j ^ ) 6

Resposta

Letra a

Exercício Resolvido #6

Elaboração Própria

Encontre a posição do centro de massa da chapa abaixo de raio R , sabendo que foi feito um furo dela de raio r posicionado como indicado na figura. Considere também que a chapa é homogênea.

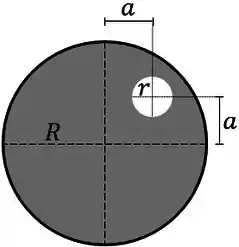
Passo 1

Nesse exercício temos um problema. Normalmente quando vamos achar o centro de massa separamos em retângulos certo? Tendo círculos ali não tem problema, o centro de massa de um círculo é no seu centro. O grande problema é aquele buraco.

Quando estivermos lidando com objetos que perdem um pedaço, podemos considerar o sistema como sendo o objeto original+furo, onde o furo tem massa negativa, como vimos na teoria.

Passo 2

Como resolvemos isso então?

Repara que temos dois círculos, então colocando o eixo cartesiano como mostrado abaixo

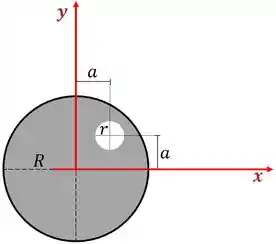
Vamos ter

C i r c u l o   d e   r a i o   R x 1 = 0 y 1 = 0 e A 1 = π . R 2

C i r c u l o   d e   r a i o   r x 2 = a y 2 = a e A 2 = π . r 2

Como ele não determinou os eixos, não importa qual eixo vou escolher. Eu decidi pelo eixo que passa pelo centro do disco maior para termos contas mais fáceis, mas não faz diferença.

Passo 3

Pela fórmula do centro de massa, a posição do centro de massa no eixo x é

x C M = A 1 ⋅ x 1 + A 2 ⋅ x 2 A 1 + A 2

x C M = π R 2 ⋅ 0 + - π r 2 ⋅ a π R 2 - π r 2

x C M = - a r 2 R 2 - r 2

Repara o sinal negativo para o disco de raio r !!

Passo 4

A posição do centro de massa no eixo y é

y C M = π R 2 ⋅ 0 + - π r 2 ⋅ a π R 2 - π r 2

y C M = - a r 2 R 2 - r 2

Passo 5

Então o vetor do centro de massa fica

r → C M = - a r 2 R 2 - r 2 i ^ - a r 2 R 2 - r 2 j ^

No sistema de eixos que escolhemos.

Uma forma de escrever isso onde o eixo não importe é deixar indicado que

“O centro de massa encontra-se a a r 2 / R 2 - r 2 abaixo e a a r 2 / R 2 - r 2 para esquerda do centro do disco maior”

Resposta

r → C M = - a r 2 R 2 - r 2 i ^ - a r 2 R 2 - r 2 j ^

“O centro de massa encontra-se a a r 2 / R 2 - r 2 abaixo e a a r 2 / R 2 - r 2 para esquerda do centro do disco maior”

Exercício Resolvido #7

UFRJ – 2ª Prova – 2012.1

Um arame homogêneo e uniforme, de espessura desprezível, é moldado na forma de um quadrado de aresta a . Retira-se então um segmento de comprimento a / 2 de duas arestas , reduzindo-as à metade, como mostra a figura. No novo sistema a distância do centro de massa à origem é igual a,

a   3 7 2 a

( b )   4 9 2 a

c   1 4 2 a

( d )   3 8 2 a

( e )   1 3 2 a

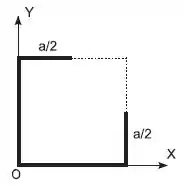
Passo 1

Para achar a distância do centro de massa até a origem devemos achar a posição do centro de massa e fazer o módulo desse vetor.

Ao usar arames, vamos considerar em vez da massa, o seu comprimento. Isso porque a massa e o comprimento são proporcionais, então no cálculo do centro de massa não altera o resultado.

O eixo cartesiano já foi dado pelo enunciado, então vamos nos basear nele.

Repara que o novo sistema é composto por 4 arames, vamos numera-los para nos organizar.

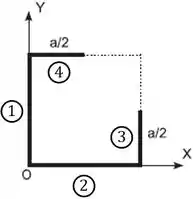
Passo 2

Lembra que o centro de massa de um arame é no seu “meio”? Então:

E i x o   x x 1 = 0 x 2 = a 2 x 3 = a x 4 = a / 2 2 = a 4

E i x o   y y 1 = a 2 y 2 = 0 y 3 = a / 2 2 y 4 = a

Passo 3

Usando a fórmula para as coordenadas do centro de massa vamos ter

x C M = x 1 ⋅ L 1 + x 2 ⋅ L 2 + x 3 ⋅ L 3 + x 4 ⋅ L 4 L 1 + L 2 + L 3 + L 4

Lembrando que

L 1 = L 2 = a

L 3 = L 4 = a 2

Assim

x C M = 0 ⋅ a + a / 2 ⋅ a + a ⋅ a / 2 + a / 4 ⋅ a / 2 2 a + 2 ⋅ a / 2

x C M = a 2 / 2 + a 2 / 2 + a 2 / 8 2 a + a

x C M = 3 a 8

Passo 4

Agora fazendo no eixo y

y C M = y 1 ⋅ L 1 + y 2 ⋅ L 2 + y 3 ⋅ L 3 + y 4 ⋅ L 4 L 1 + L 2 + L 3 + L 4

Então teremos

y C M = a / 2 ⋅ a + 0 ⋅ a + a / 4 ⋅ a / 2 + a ⋅ a / 2 2 a + 2 ⋅ a / 2

y C M = a 2 / 2 + a 2 / 8 + a 2 / 2 2 a + a

y C M = 3 a 8

Passo 5

O vetor posição do centro de massa vai ser

r → C M = x C M i ^ + y C M j ^

r → C M = 3 a 8 i ^ + 3 a 8 j ^

A distância do centro de massa até a origem é o módulo do vetor posição, já que o vetor posição parte da origem.

r → C M 2 = 3 a 8 2 + 3 a 8 2

r → C M 2 = 9 a 2 64 + 9 a 2 64

r → C M 2 = 18 a 2 64

r → C M = 3 8 a 2

Resposta

Letra d

Exercício Resolvido #8

Elaboração Própria

Encontre a posição do centro de massa do objeto desenhado na figura abaixo, sabendo que ele é constituído por 6 pedações de arames homogêneo feitos do mesmo material.

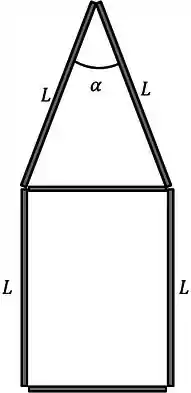
Passo 1

Assim como quando usamos fios, ao usar arames, vamos considerar em vez da massa, o seu comprimento. Isso porque a massa e o comprimento são proporcionais, então no cálculo do centro de massa não altera o resultado.

Vamos colocar o eixo cartesiano como na figura abaixo.

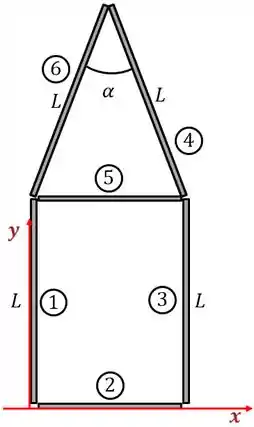
Repara que temos 6 barras, uma coisa para ajudar a organizar a resolução é nomear cada barra. Para achar o centro de massa precisamos da posição do meio de cada barra para usar na fórmula. Não temos o comprimento de todas elas.

Passo 2

Vamos começar encontrando o comprimento das barras 2 e 5 . Vamos chamar seu comprimento de d . Olha o triangulo 6 , 5,4

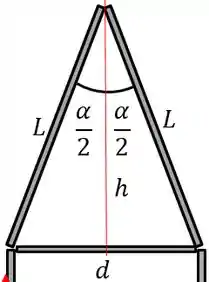
Esse triangulo é isósceles, então posso separar o ângulo α como fiz na figura. Usando trigonometria encontramos

d / 2 L = sen ⁡ α 2

d = 2 L sen ⁡ α 2

Passo 3

Vamos começar achando a posição do centro de massa da barra 6 .

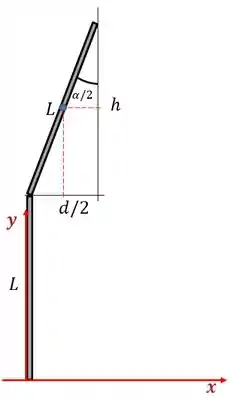
Repara que a posição vertical dele vai ser

y 6 = h 2 + L

Que é a metade da “altura” da barra h / 2 mais a a altura onde a barra está L .

Vamos achar h então, usando trigonometria de novo

h L = cos ⁡ α 2

h = L cos ⁡ α 2

Vamos ter

y 6 = L 2 cos ⁡ α 2 + L

Passo 4

Agora vamos achar a posição horizontal dele, que vai ser

x 6 = d / 2 2 = d 4

Isso porque ela fica na metade do “comprimento” da barra, e esse “comprimento” é d / 2 .

Então

x 6 = L 2 sen ⁡ α 2

É importante entender que em uma barra o centro de massa está na metade do comprimento e na metade da altura da barra.

Passo 5

Vamos agora para a barra 4

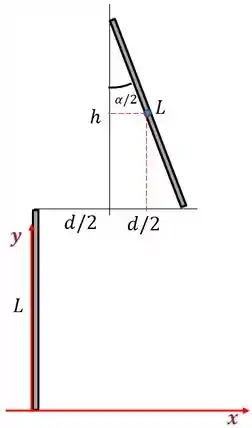
a altura do centro de massa dessa barra vai ser igual a da barra 6

y 4 = y 6 = L 2 cos ⁡ α 2 + L

Passo 6

A posição horizontal dele vai ser

x 4 = d 2 + d / 2 2 = 3 d 4

Então

x 4 = 3 L 2 sen ⁡ α 2

Passo 7

O centro de massa das outras barras é mais fácil de fazer, segue um desenho da posição de cada um

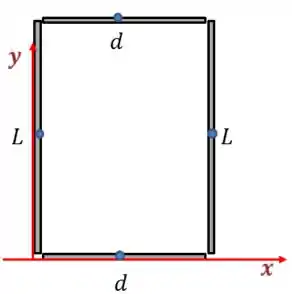
Vamos ter,

B a r r a   1 x 1 = 0 y 1 = L 2

B a r r a   2 x 2 = d 2 = L sen ⁡ α 2 y 2 = 0

B a r r a   3 x 3 = d = 2 L sen ⁡ α 2 y 3 = L 2

B a r r a   5 x 5 = d 2 = L sen ⁡ α 2 y 5 = L

Passo 8

Vamos agora juntar isso tudo, começando pela posição horizontal

e i x o   x x 1 = 0 x 2 = L sen ⁡ α 2 x 3 = 2 L sen ⁡ α 2 x 4 = 3 L 2 sen ⁡ α 2 x 5 = L sen ⁡ α 2 x 6 = L 2 sen ⁡ α 2

x C M = x 1 ⋅ L 1 + x 2 ⋅ L 2 + x 3 ⋅ L 3 + x 4 ⋅ L 4 + x 5 ⋅ L 5 + x 6 ⋅ L 6 L 1 + L 2 + L 3 + L 4 + L 5 + L 6

Sabemos que

L 2 = L 5 = d = 2 L sen ⁡ α 2

L 1 = L 3 = L 4 = L 6 = L

x C M = L sen ⁡ α 2 2 L sen ⁡ α 2 + 2 L sen ⁡ α 2 L + 3 L 2 sen ⁡ α 2 L + L sen ⁡ α 2 2 L sen ⁡ α 2 + L 2 sen ⁡ α 2 L 4 L + 2 ⋅ 2 L sen ⁡ α 2

x C M = 2 L 2 sen 2 ⁡ α 2 + 2 L 2 sen ⁡ α 2 + 3 L 2 2 sen ⁡ α 2 + 2 L 2 sen 2 ⁡ α 2 + L 2 2 sen ⁡ α 2 4 L + 4 L sen ⁡ α 2

x C M = 4 L 2 sen 2 ⁡ α 2 + 4 L 2 sen ⁡ α 2 4 L + 4 L sen ⁡ α 2

Colocando o que der para colocar em evidência

x C M = 4 L 2 sen ⁡ α 2 sen ⁡ α 2 + 1 4 L 1 + sen ⁡ α 2

x C M = L sen ⁡ α 2

Ufa né? Deixa eu te falar uma parada, eu fiz dessa forma mega trabalhosa para te mostrar como fazer essa questão e entender bem a matéria, afinal estamos nos exercícios de fixação.

Mas aqui vai a dica para esse tipo de questão

Podíamos simplesmente fazer

x C M = d 2 = L sen ⁡ α 2

Porque ele é simétrico, mas é importante fazer essas contas para ficar craque em centro de massa. Vamos continuar a questão.

Passo 9

Vamos agora achar ao longo do eixo y

e i x o   y y 1 = L 2 y 2 = 0 y 3 = L 2 y 4 = L 2 cos ⁡ α 2 + L y 5 = L y 6 = L 2 cos ⁡ α 2 + L

y C M = y 1 ⋅ L 1 + y 2 ⋅ L 2 + y 3 ⋅ L 3 + y 4 ⋅ L 4 + y 5 ⋅ L 5 + y 6 ⋅ L 6 L 1 + L 2 + L 3 + L 4 + L 5 + L 6

Sabemos que

L 2 = L 5 = d = 2 L sen ⁡ α 2

L 1 = L 3 = L 4 = L 6 = L

y C M = L 2 L + L 2 L + L 2 cos ⁡ α 2 + L L + L 2 L sen ⁡ α 2 + L 2 cos ⁡ α 2 + L L 4 L + 2 ⋅ 2 L sen ⁡ α 2

y C M = L 2 2 + L 2 2 + L 2 2 cos ⁡ α 2 + L 2 + 2 L 2 sen ⁡ α 2 + L 2 2 cos ⁡ α 2 + L 2 4 L + 4 L sen ⁡ α 2

y C M = 3 L 2 + L 2 cos ⁡ α 2 + 2 L 2 sen ⁡ α 2 4 L + 4 L sen ⁡ α 2

Colocando o que der para colocar em evidência

y C M = 2 L 2 3 2 + 1 2 cos ⁡ α 2 + sen ⁡ α 2 4 L 1 + sen ⁡ α 2

y C M = L 2 ⋅ 3 2 + 1 2 cos ⁡ α 2 + sen ⁡ α 2 1 + sen ⁡ α 2

Passo 10

Vamos escrever a posição do centro de massa na forma vetorial.

r → C M = x C M i ^ + y C M j ^

r → C M = L sen ⁡ α 2 i ^ + L 2 ⋅ 3 2 + 1 2 cos ⁡ α 2 + sen ⁡ α 2 1 + sen ⁡ α 2 j ^

Resposta

r → C M = L sen ⁡ α 2 i ^ + L 2 ⋅ 3 2 + 1 2 cos ⁡ α 2 + sen ⁡ α 2 1 + sen ⁡ α 2 j ^

Exercícios de Livros Relacionados

A Fig. 9-35 mostra um sistema de três partículas de massas m 1 = 3,0k g , m 2 = 4,0k g e m 3 = 8,0k g . As escalas do gráfico são definidas por x s = 2,0m e y s = 2,0m . Quais são (a) a coordenada x e
Um pedaço uniforme de folha de metal é moldado conforme mostrado na Figura P8.34. Calcule as coordenadas x e y do centro de massa da folha.
Uma haste de 30,0c m de comprimento tem densidade linear (massa por comprimento) definida por λ=50,0+20,0x em que x é a distância a partir de uma extremidade, medida em metros, e λ expressa g r a m a
Duas partículas de 3,0k g têm velocidades v → 1 = 2,0 m s i ^ + 3,0 m s j ^ e v → 2 = 4,0 m s i ^ - 6,0 m s j ^ . Encontre a velocidade do centro de massa do sistema.
Quatro corpos estão situados ao longo do eixo y da seguinte forma: um de 2,00k g está a + 3,00m , um de 3,00k g está a + 2,50m , o terceiro, de 2,50k g , está na origem, e o quarto, de 4,00k g , está