Lista de Aplicações Cálculo 1 - UnB de Cálculo 1 da UnB - Lista 9

Durante o processo de tosse, provocado pela presença a traqueia de algum corpo estranho, a traqueia se contrai com o objetivo de aumentar o fluxo de ar através dela, e assim tornar mais eficiente o método de expulsão do corpo estranho. Segundo Pouseiulle, indicando por o raio da traqueia em estado normal e por o seu raio durante a tosse, o fluxo de ar na traqueia pode ser modelado por:

Onde K é uma constante positiva.

1. Determine os pontos críticos de no intervalo
2. Determine os intervalos de crescimento e de decrescimento de
3. Determine os intervalos em que o gráfico de é côncavo para cima ou para baixo.
4. Use os itens anteriores para esboçar o gráfico de no caso em que

Conforme ilustra a figura abaixo, as áreas dos retângulos inscritos na circunferência podemos ser calculadas por meio da função , com

1. Calcule os pontos críticos da função no intervalo
2. Determine os intervalos de crescimento e os de decrescimento da função
3. Determine os intervalos em que a concavidade do gráfico de é voltada para baixo e os intervalo em que a concavidade é voltada para cima
4. Esboce o gráfico de

Suponha que o número de milhares de pessoas infectadas por um vírus seja modelado pela função em que e são constantes e o tempo é medido em anos. Suponha ainda que, no instante , nove mil pessoas estavam infectadas, uns anos depois esse número atingiu um valor mínimo e, em seguida, cresceu até atingir um valor máximo para .

Determine as constantes e a partir das informações dadas.

Determine o número de pessoas infectadas anos depois do instante .

Determine a concavidade de e, em seguida, esboce o seu gráfico para

O mecanismo de suspensão dos automóveis consiste num sistema composto de uma mola e de um amortecedor. Denotando por s(t) a posição vertical de um veículo de massa em relação a posição de equilíbrio, temos que a força da mola é dada, pela lei de Hooke, por e a força do amortecedor é dada por , onde é a velocidade instantânea e a constante é denominada viscosidade do amortecedor. Como a força resultante é , pela Segunda Lei de Newton, temos que

para . Suponha que, em unidades adequadas, e e considere

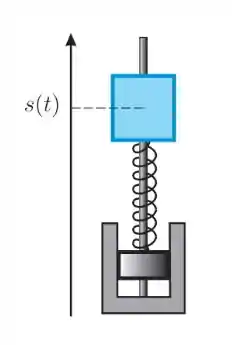
(a) Calcule e e verifique que a equação é satisfeita.

(b) Calcule os pontos críticos de e determine seus extremos

locais e seus intervalos de crescimento e decrescimento.

(c) Determine os pontos de inflexão de e os intervalos

onde a concavidade é voltada para cima e onde é voltada para baixo.

(d) Determine as assíntotas de e, em seguida, esboce o seu gráfico.

Considere duas cargas elétricas com carga unitária e positiva, fixadas num eixo perpendicular a uma parede, como na figura abaixo. O potencial elétrico gerado por essas duas partículas num ponto ao longo desse eixo é dado, em unidades convenientes, pela

seguinte função

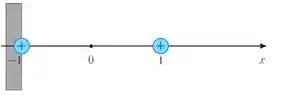
(a) Verifique que o potencial elétrico é dado por

(b) Calcule a força exercida numa partícula de carga unitária posicionada em , dada

por .

(c) Calcule os pontos críticos de e determine seus extremos locais e seus intervalos

de crescimento e decrescimento. A força se anula em algum ponto?

(d) Determine os pontos de inflexão de e seus intervalos de concavidade para cima

e para baixo.

(e) Determine as assíntotas verticais e horizontais de e esboce seu gráfico.